Pythonで３点どうしの位置をあわせる　座標系を一致させる

CTなど画像データから作った立体は、撮影時に設定した位置データに従うので、
並べるととんでもなく離れていることがあります。

ここでは、Pythonを使って２つの離れた表面データの位置をあわせる方法を紹介します。

１．３点を使って表面を合わせるということ

この時、基準の点をとって位置を合わせてやる事ができます。

立体の点を決めるのは３点になります。

いろいろな合わせ方がありますが、ここでは座標軸を合わせる方法を行います。

「座標軸をあわせる」というと難しいですが

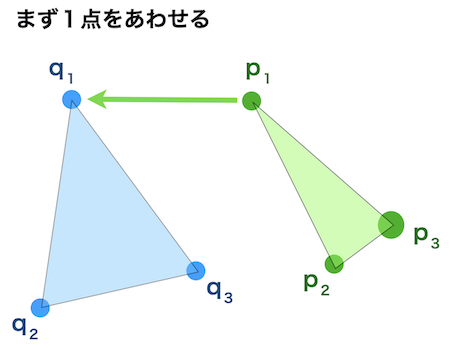
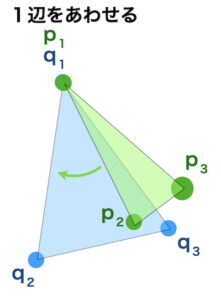
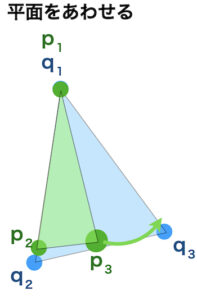
１点をあわせる
↓
２点の直線をあわせる
↓
３点の面をあわせる

ことで全体を一致させます。
 

２．ベクトルを使った計算方法

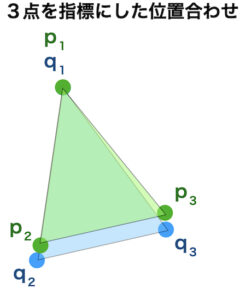
まず２つの表面で３点をとります。

合わせに行く表面データPの点の名前を\(p_1, p_2, p_3\)とします
基準面の表面データQの点を\(q_1, q_2, q_3\)とします。

表面データPで座標を設定します。
座標の決め方はPとQについて同じなので、
表面データPについて説明します。

\(p_1\) ⇒ \(p_2\)のベクトルを \(\overrightarrow{px} \)
\(p_1\) ⇒ \(p_3\)のベクトルを \(\overrightarrow{py} \)
とします。

\(p_1\) を原点
\(\overrightarrow{px} \)方向をx軸
\(\overrightarrow{px} \)と\(\overrightarrow{py} \)とに垂直な軸がz軸
z軸とx軸に垂直な軸がy軸

とします。

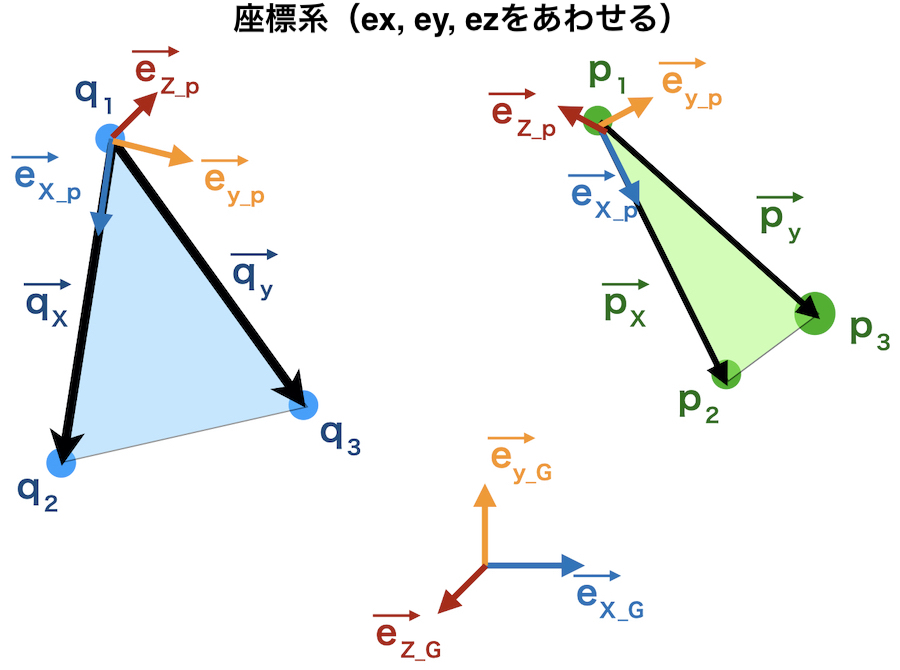
これら表面データP, Qと絶対座標系の単位ベクトルをあわせることで、３点の移動行列を求めます。

x軸の単位ベクトル\(\overrightarrow{ex_p} \)は
\(\displaystyle \overrightarrow{ex_p} = \frac{\overrightarrow{px}}{|\overrightarrow{px} |}\)

\(\overrightarrow{px}\)と\(\overrightarrow{py}\)に垂直なベクトルは２つの外積になるので、
z軸の単位ベクトルは
\(\displaystyle \overrightarrow{ez_p} = \frac{\overrightarrow{px} \times \overrightarrow{py}}{|\overrightarrow{px} \times \overrightarrow{py}|}\)

y軸の単位ベクトルは
\(\displaystyle \overrightarrow{ey_p} = \overrightarrow{ez_p} \times \overrightarrow{ex_p}\)
です。

ここで外積を逆にしてしまって、
\(\displaystyle \overrightarrow{ey_p} = \overrightarrow{ex_p} \times \overrightarrow{ez_p}\)
としてしまうと座標系にならないことに注意が必要です。

ここでex, ey, ezを縦に書いた行列
\(M_p = \begin{pmatrix}
\overrightarrow{ex_p} & \overrightarrow{ey_p} & \overrightarrow{ey_p}
\end{pmatrix}\)

は回転行列です。

ちなみにここで
単位ベクトルはx, y, zの値があるため、
\(\overrightarrow{ex_p} =
\left(
\begin{array}{c}
ex_{p1} \\
ex_{p2} \\
ex_{p3}
\end{array}
\right)
\) \(\overrightarrow{ey_p} =
\left(
\begin{array}{c}
ey_{p1} \\
ey_{p2} \\
ey_{p3}
\end{array}
\right)
\) \(\overrightarrow{ez_p} =
\left(
\begin{array}{c}
ez_{p1} \\
ez_{p2} \\
ez_{p3}
\end{array}
\right)
\)

\(M_p = \begin{pmatrix}
ex_{p1} & ey_{p1} & ez_{p1} \\
ex_{p2} & ey_{p2} & ez_{p2} \\
ex_{p3} & ey_{p3} & ez_{p3}
\end{pmatrix}\)

と書けます。

３．表面データ上の点で考える

わかりやすいように、表面データP上の点を表面データQ上に合わせる流れで説明します。

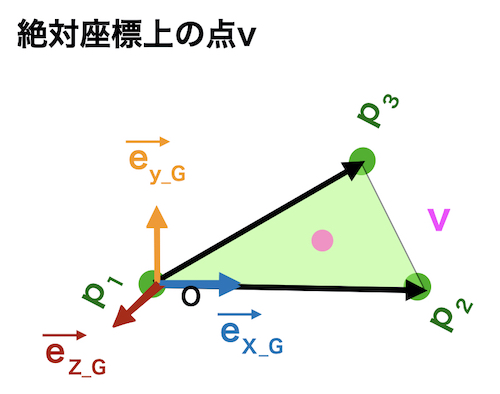
絶対座標上の点\(v\)
を表面データP上の同じ座標位置に持っていくには
まずベクトルを回転させます。

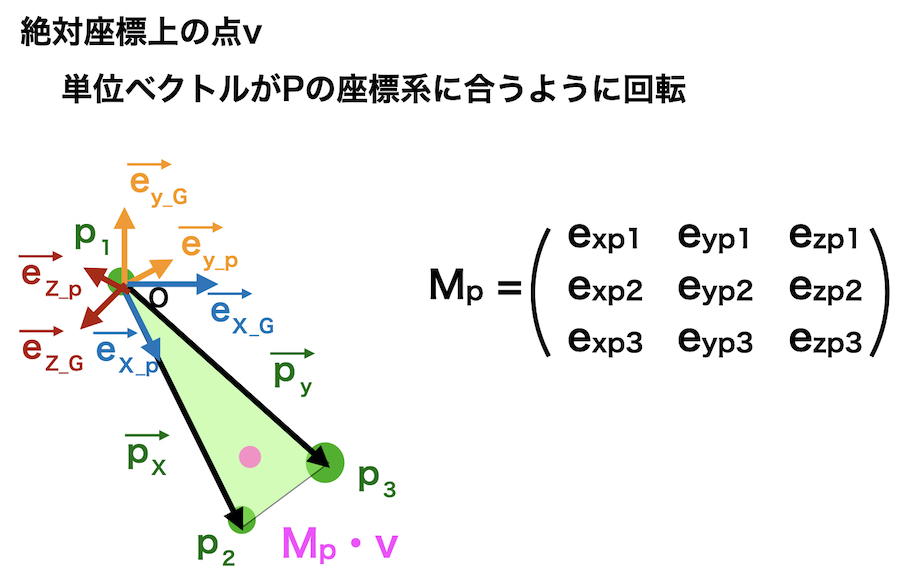
そして原点がPの原点\(p_1\)に合うように移動させます

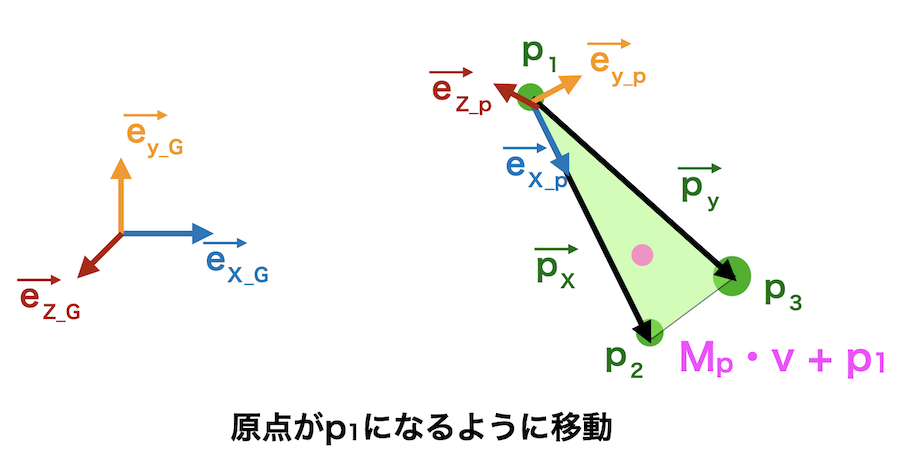
\(M_p \cdot v + p_1\)

逆に表面データP上の点 s を絶対座標に移動させるには
まず原点を絶対座標系に合わせるように移動させます。

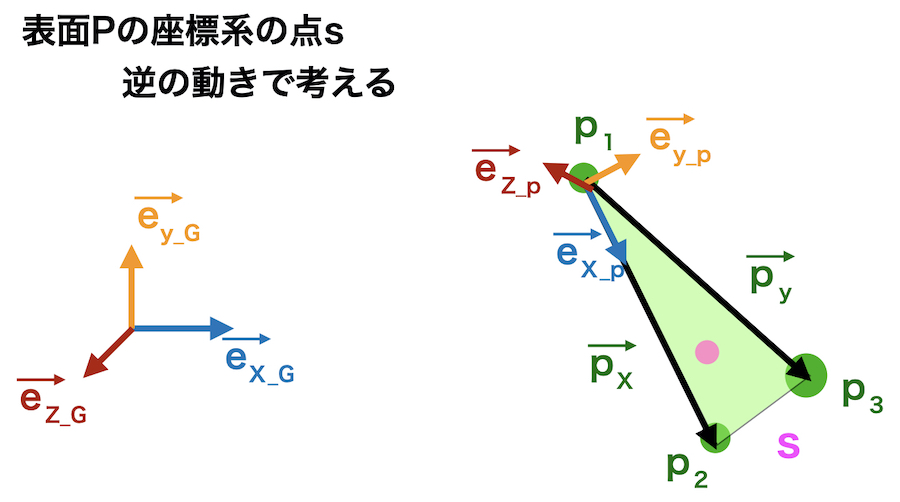
次に先程とは逆の回転行列で回転させます。
回転行列の逆行列は転置行列なので、ここでは転移行列をかけます。

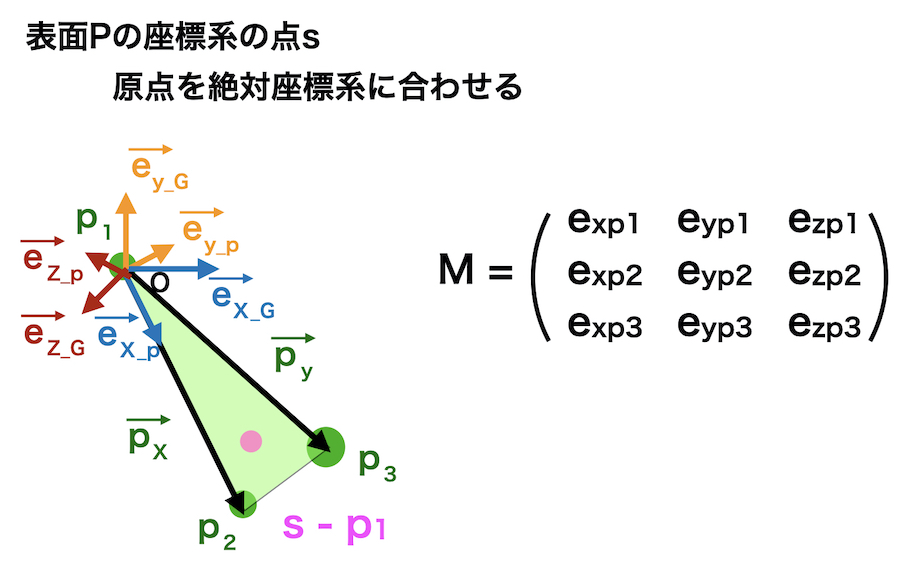
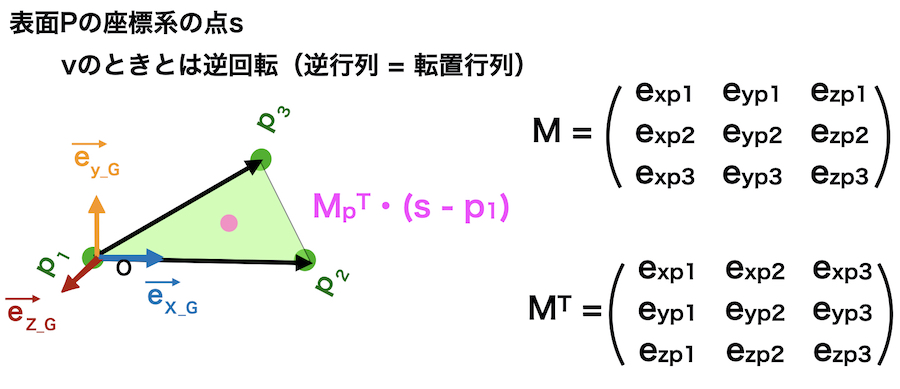
\(M_p ^{\mathrm{T}} \cdot (s – p_1)\)

一方で絶対座標上点 u　を一致する表面データQ上に移動させるには

\(M_q \cdot u + q_1\)

ですから、まとめると
表面データP上の点piを表面データQ上に移動させるには

\(M_q \cdot (M_p ^{\mathrm{T}} \cdot (pi – p_1)) + q_1\)

\(M_q \cdot Mp ^{\mathrm{T}} \cdot pi – M_q \cdot M_p ^{\mathrm{T}} \cdot p_1 + q_1\)
となります。

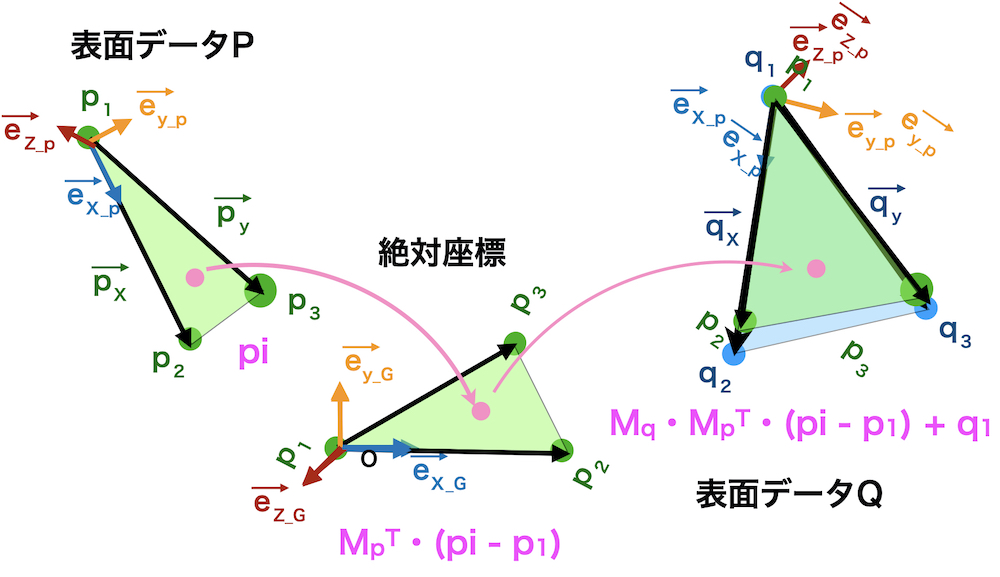
これを座標でかくと
これは回転の成分 と
\(M = M_q \cdot Mp ^{\mathrm{T}}\)
移動の成分
\(t = – M_q \cdot M_p ^{\mathrm{T}} \cdot p_1 + q_1\)
とすると
\(M \cdot p_i + t\)

となっています。

座標があっちいったり、こっちいったりで混乱しちゃいますね

乗り物みたいに、自分が表面データの上にのって動いていくのを想像すれば少しはわかりやすくなるよ。

４．Pythonのコードで書く

この流れを書くと

import numpy as np

def transform_matrix(p1, p2, p3, q1, q2, q3):
    """
    入力パラメータ: P上の点p1, p2, p3の座標、Q上のq1, q2, q3の座標
    出力パラメータ: 回転行列 M, 移動行列t
    """

    #表面Pについてパラメータを計算
    #px, pyのベクトルを計算する
    px = p2 - p1
    py = p3 - p1
    #単位ベクトルex, ey, ezで計算する
    ex_p = px / np.linalg.norm(px)
    ez_p = np.cross(px, py) / np.linalg.norm(np.cross(px, py))
    ey_p = np.cross(ez_p, ex_p)
    #縦の単位ベクトルを横に並べたベクトルが回転行列
    Mp = np.array([ex_p, ey_p, ez_p]).T
    
    #同様に表面Qについても計算
    qx = q2 - q1
    qy = q3 - q1
    ex_q = qx / np.linalg.norm(qx)
    ez_q = np.cross(qx, qy) / np.linalg.norm(np.cross(qx, qy))
    ey_q = np.cross(ez_q, ex_q)
    Mq = np.array([ex_q, ey_q, ez_q]).T
    
    #ベクトルの式より、表面P⇒Qに移動する回転行列、移動行列を計算
    M = np.dot(Mq, Mp.T)
    t = - np.dot(np.dot(Mq, Mp.T), p1) + q1
    return M, t

となります。

５．CTデータで検証 (numpy-stlを使用)

例として、肩甲骨の骨のstlデータを使用します。

左と右では左右対称なので左をひっくり返します。

MeshLabの「Filters」→ 「Normals, Curvatures and Orientation」→「Flip and/or swap axis」
を使ってひっくり返します。

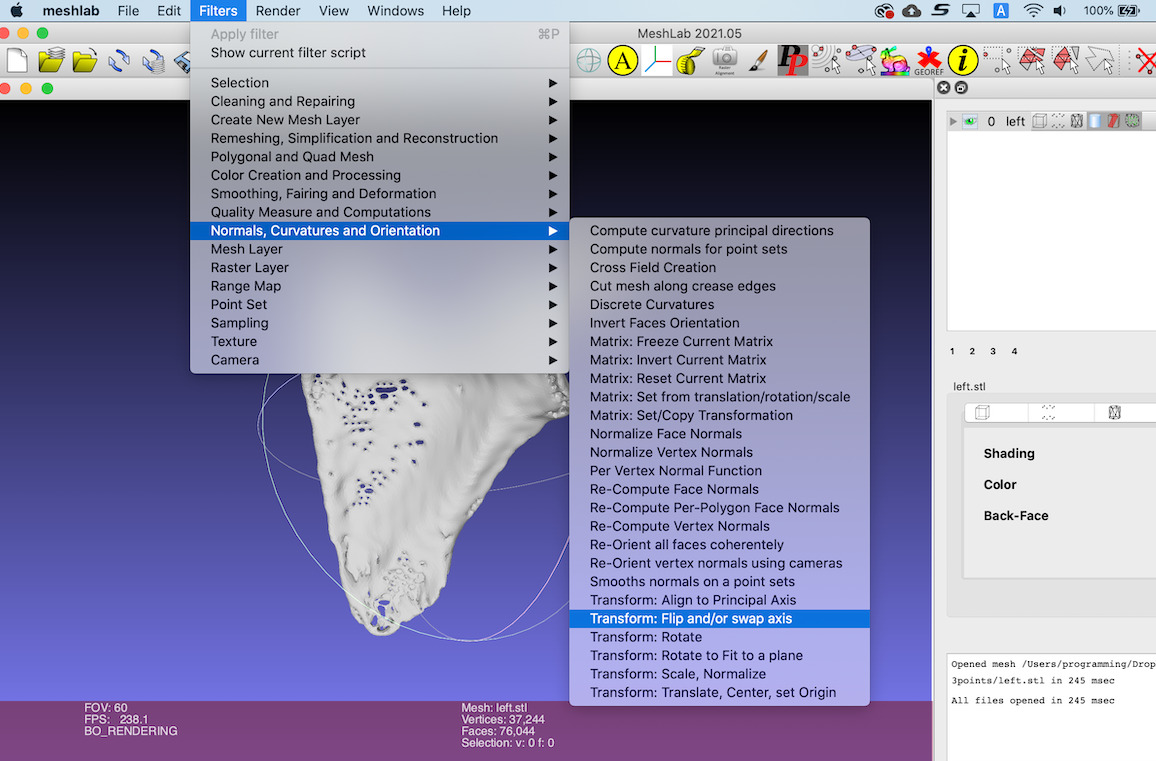
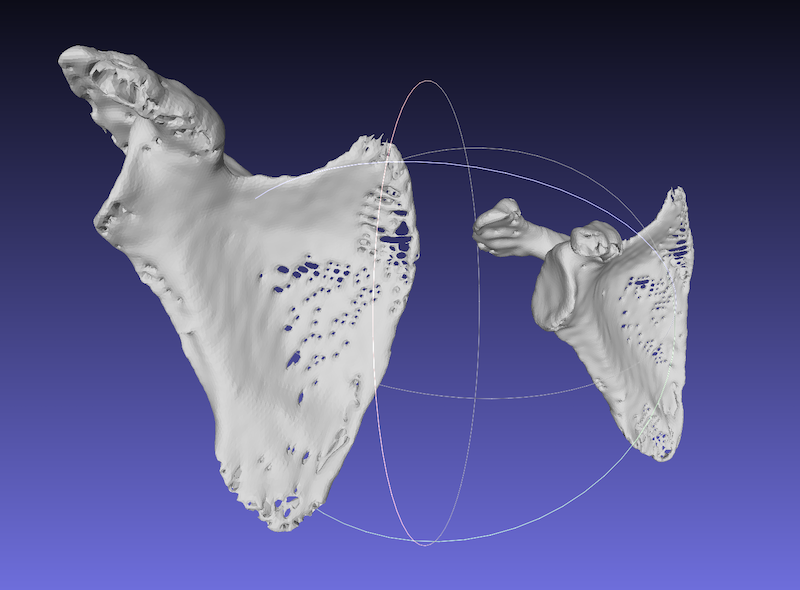
右と左（反転）の肩甲骨です。　位置がずれています。

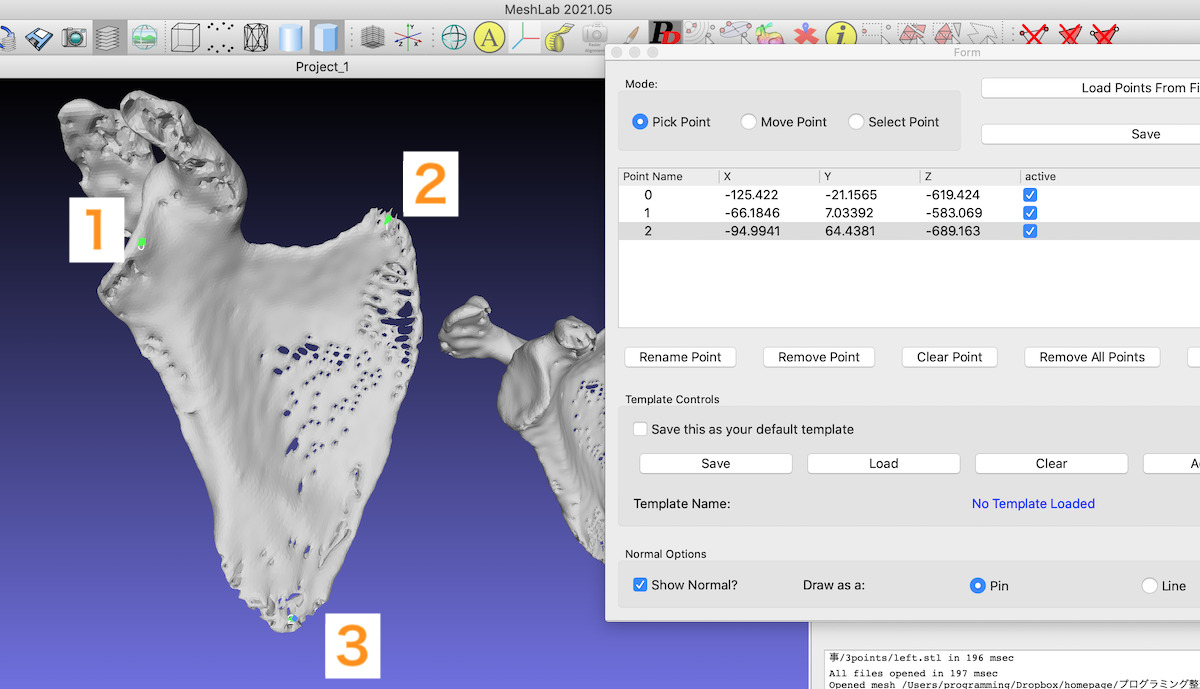
右で点を３つとり、right.ppファイルで保存します。

左でも点を３つとり、left.ppファイルで保存します。

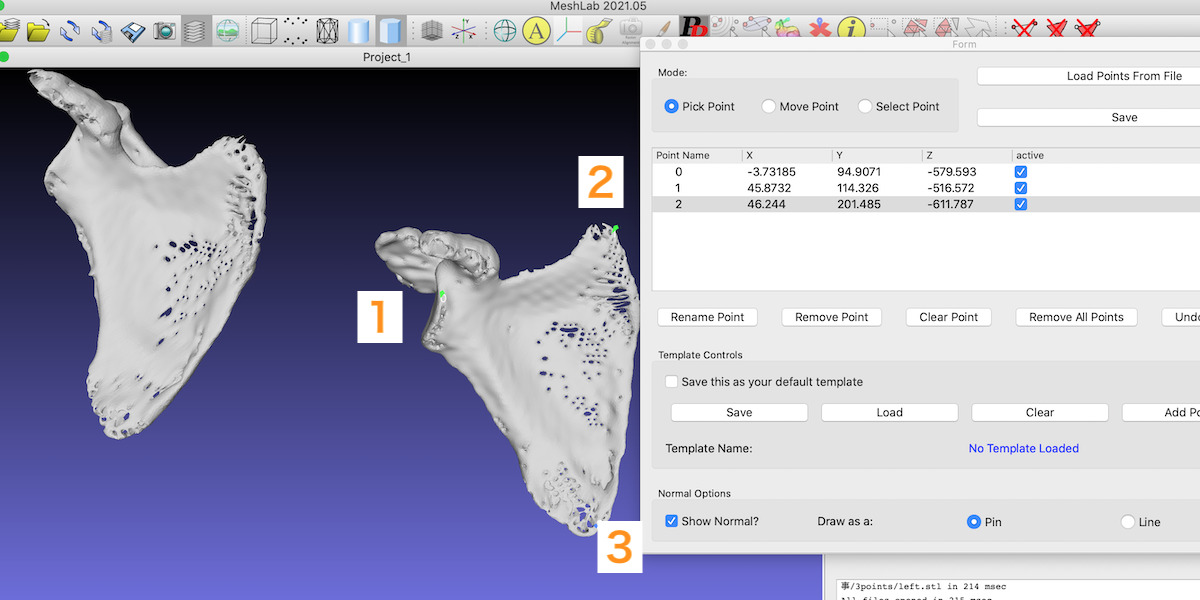
点をとる順番を一致させることが重要です。

これら表面データとポイント座標のファイル(.ppファイル)を作業フォルダにおいて以下のファイルを実行します。

import point_class
import rough_match
"""ppファイルから3点を読み取る"""
right_points = point_class.MeshlabPp('right.pp')
# right.stlの3点をright_pointsに入れる
left_points = point_class.MeshlabPp('left.pp')
# left.stlの3点をleft_pointsに入れる
p1, p2, p3 = right_points.point_list
q1, q2, q3 = left_points.point_list
M, t = rough_match.transform_matrix(p1, p2, p3, q1, q2, q3)
#２つの表面からの3点ずつを入力し、回転行列と移動行列を計算する

print(M)
#回転行列
# [[ 0.9590293  -0.05833918 -0.27723519]
#  [-0.01219987  0.96915644 -0.24614419]
#  [ 0.28304412  0.23944172  0.92873769]]


print(t)
# 移動行列
# [-56.40921238 -38.58660633  36.25468863]

※.ppファイルからの点の抽出は以下で述べています
⇒ MeshLabで点をとってデータを抽出する方法

位置合わせの結果は外部パッケージのnumpy-stlをインストールすることで視覚的に確認できます。

numpy-stlの使用には

でインストールする必要があります。

right.stlを回転行列\(M\), 移動行列\(t\)で移動します。

import numpy as np
from stl import mesh

right_stl = mesh.Mesh.from_file('right.stl')
transform_matrix = np.identity(4)
transform_matrix[:3, :3] = M
transform_matrix[:3, 3] = t
print(transform_matrix)
# [[ 9.59029296e-01 -5.83391829e-02 -2.77235188e-01 -5.64092124e+01]
#  [-1.21998734e-02  9.69156438e-01 -2.46144190e-01 -3.85866063e+01]
#  [ 2.83044118e-01  2.39441723e-01  9.28737685e-01  3.62546886e+01]
#  [ 0.00000000e+00  0.00000000e+00  0.00000000e+00  1.00000000e+00]]
right_stl.transform(transform_matrix)
right_stl.save('right_trans.stl')

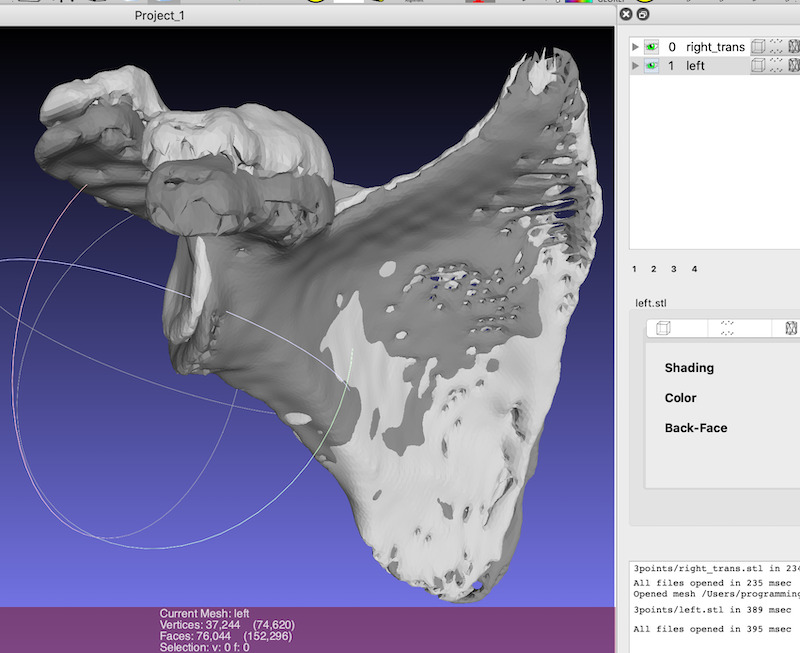
３点をもとにした移動でもかなり一致する事がわかります。

だいぶ一致してますけど、もうちょっとピッタリ合わせる方法ないんですか？

点全体をあわせるICPという方法があるよ。でもそれを使うにはこの方法のようにして事前にある程度合わせておくことが必要なんだ。
また説明していくね。

補足：Meshlabでの点の読み取り

Meshlabで点を読む方法は

「Meshlabで表面上の点を読み取る」
「ソフトウェアで書き出したファイルの読み取り」
で説明しています。

ここでは以下の書き出した.ppファイルの読み取りにpoint_class.pyを使用しています。

import numpy as np

class MeshlabPp(object):
    """
    ppファイルをobjectに入れて読みこむ
    .point_listで読み込んだポイントの座標をリストにして返す
    """
    def __init__(self, file_name):
        self.point_list = read_pp(file_name)

def read_pp(file_name):
    point_list = []
    with open(file_name) as f:
        line = f.readline()
        while line:
            inside_line = line[line.find('<') + 1: line.find('/>')]
            words = inside_line.split(' ')
            if words[0] == 'point':
                for word in words:
                    if 'x=' in word:
                        x = float(word.split('"')[1])
                    elif 'y=' in word:
                        y = float(word.split('"')[1])
                    elif 'z=' in word:
                        z = float(word.split('"')[1])
                point_list.append(np.array([x, y, z]))
            line = f.readline()
    return point_list