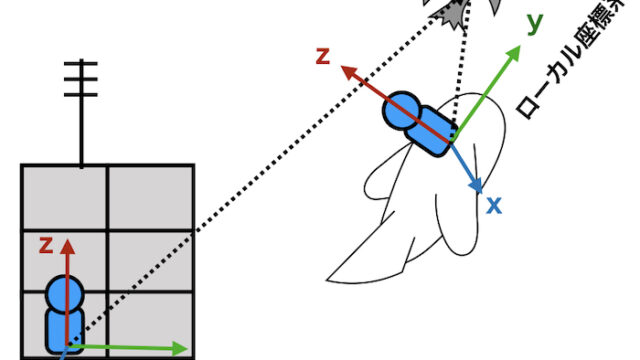
整形外科では関節を扱います。
関節の骨の形状を平面に近似して考えることがあります。
例えば
- 膝関節の脛骨側
- 肩関節の肩甲骨側
- 脊椎の椎間関節
などは代表的な平面の形状をしている骨です。
ここでは表面データから平面を近似する方法を記載します。
平面近似の方法とそのスクリプト
平面近似のプログラムの流れ
近似式の導出は少し複雑なので、先に計算方法とスクリプトを書きます。
点群 \(p_i (i=1 から n)\)
にフィットする平面は
重心
\(com = \displaystyle \frac {1}{N}\displaystyle \sum_i p_i\)
を通ります。
重心を原点に移動するように点群を移動し、
\(q_i = p_i – com\)
\(Q =\displaystyle \sum_i^{n} q_i \cdot q_i^{\mathrm{T}} \)
とした3×3行列Qの
固有値\(\lambda\)が最小となるような固有ベクトル\(v\)
が法線ベクトルとなります。
これをPythonスクリプトで記載します。
pythonファイルをfitting.pyとして以下の用に記載します。
import numpy as np
def fit_plane(point_cloud):
"""
入力
point_cloud : xyzのリスト numpy.array型
出力
plane_v : 法線ベクトルの向き(単位ベクトル)
com : 重心 近似平面が通る点
"""
com = np.sum(point_cloud, axis=0) / len(point_cloud)
# 重心を計算
q = point_cloud - com
# 重心を原点に移動し、同様に全点群を平行移動する pythonのブロードキャスト機能使用
Q = np.dot(q.T, q)
# 3x3行列を計算する 行列計算で和の形になるため総和になる
la, vectors = np.linalg.eig(Q)
# 固有値、固有ベクトルを計算 固有ベクトルは縦のベクトルが横に並ぶ形式
plane_v = vectors.T[np.argmin(la)]
# 固有値が最小となるベクトルの成分を抽出
return plane_v, com
これで近似平面の法線ベクトルと通過点である重心が計算できます。
平面近似の例 膝の関節
例として
膝の関節の面を平面近似します。
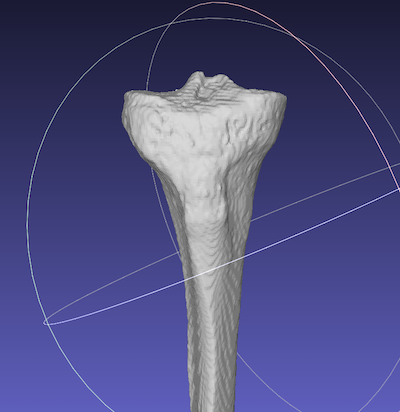
Meshlabで膝の関節の表面データを取り出し、”joint.stl”で保存します。

緑:”joint.stl”
import numpy as np
import fitting
from stl import mesh
joint_stl = mesh.Mesh.from_file('joint.stl')
point_list = joint_stl.points.reshape([-1, 3])
v, com = fitting.fit_plane(point_list)
print(v)
[ 0.26270565 -0.32178232 0.90963835]
print(com)
[ -42.37019 -38.650146 1169.6364 ]
重心と平面を決めて平面を書き出すプログラムを書いて確認します。
fitting.draw_plane(v, com)※ 関数draw_planeは後述します。

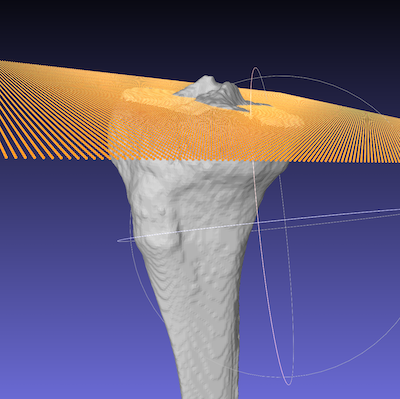
関節の面が近似できていることがわかります。
平面を点群で書き出すプログラム
確認する平面を描画する関数について説明します。
平面を点群として書き出す手順は
xy平面に点群をセットする
↓
z軸方向を向いている法線をy軸回りに\(\theta\)、z軸回りに\(\phi\)順に回転させて、
目的の法線ベクトルに合わせるようなthetaとphiを計算する。
↓
点群全体に同じ回転行列をかけて移動させる
↓
重心分平行移動する
とします。
法線ベクトルは図のようにz軸向きだったものを
y軸に\(\theta\)回転 → z軸に\(\phi\)回転として表せます。
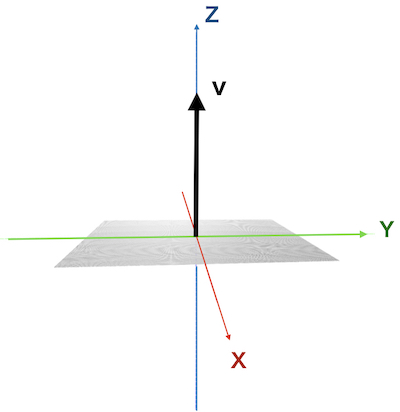

y軸回りに\(\theta\)回転させます。
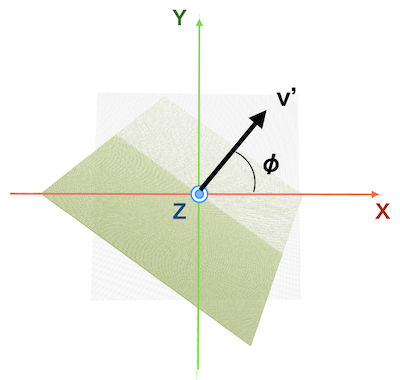
xy平面を上から見た図です。 z軸まわりに\(\phi\)回転させます
法線ベクトルの長さrとすると(定義では1です)
回転した先の法線ベクトル\(v’\)の座標は
\(z = r \cos\theta\)
\(y = r \sin\theta \sin\phi\)
\(x = r \sin\theta \cos\phi\)
となり、
\(\theta = \displaystyle \frac {z}{r} \arccos \theta\)
\(\phi = atan2 (y, x)\)
となります。
※ atan2 (x1, x2)は、y方向x1, x方向x2の\(tan\theta\)の\(\theta\)を求める関数です。
y軸回りに\(\theta\)回転する回転行列は
\(
\begin{pmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{pmatrix}\)
z軸回りに\(\phi\)回転する回転行列は
\(
\begin{pmatrix}
\cos \phi & – \sin \phi & 0 \\
\sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{pmatrix}\)
なので、これらを使って点群を回転します。
回転後の点群を重心の分、平行移動して点群を保存します。
スクリプトで書くと
def draw_plane(plane_v, com, plane_asc_name='plane.asc', d=100):
"""
入力
plane_v : 平面の表面ベクトル
com : 点群の重心位置
plane_asc_name : 点群を保存するファイル名 デフォルトは'plane.asc'
d : -dからdまで点群を描画する デフォルトは100
"""
point_cloud = []
# -dからdまでの点群をxy平面に作成する
for i in range(-d, d):
for j in range(-d, d):
point_cloud.append(np.array([i, j, 0]))
point_cloud = np.array(point_cloud)
#y軸回りにtheta回転, z軸回りにphi回転として角度を法線ベクトルの向きから計算する
theta = np.arccos(plane_v[2] / np.linalg.norm(plane_v))
phi = np.arctan2(plane_v[1], plane_v[0])
#法線を回転させるような回転行列を計算する
rotation_y = np.array([[np.cos(theta), 0, np.sin(theta)],
[0, 1, 0],
[-np.sin(theta), 0, np.cos(theta)]])
rotation_z = np.array([[np.cos(phi), -np.sin(phi), 0],
[np.sin(phi), np.cos(phi), 0],
[0, 0, 1]])
rotation_matrix = np.dot(rotation_z, rotation_y)
#点群に回転行列をかけて移動させる。numpyのブロードキャストを使用
translated_points = np.dot(rotation_matrix, point_cloud.T).T + com
#点群をMeshlabで読めるように.ascで保存する
np.savetxt('plane.asc', translated_points)
returnこのように書けます。
平面近似の計算の原理
最小二乗法と拘束条件
平面近似が固有値計算から求められる理由を説明します。
平面の方程式は、法線ベクトルの向きを
\(t = (a, b, c)\)
とし、
\(ax + by + cz = h\)
と書けます。
これは、平面上の点pを
\(p = (p_x, p_y, p_z)\)
として
\(t \cdot p = h\)
とも書けます。
法線ベクトルの長さを1と定義します。
\(\| \boldsymbol{t} \| = 1\)
を満たします。
点群をn個、i番目の点をp_iとして、
最小二乗法をつかって近似平面を求めます。
近似平面は、平面から点群の距離の2乗の総和を最小にする平面です。
そのため
\(f(t, h) = \displaystyle \sum_i (t \cdot p_i \ – h)^2\)
を最小にするtとhを求めればよいことになります。
ここで
法線ベクトルの長さは1なので
\(\| \boldsymbol{t} \| = 1\)
を変形して
\(g(t, h) = t \cdot t – 1 = 0\)
という条件がついています。
このように拘束条件がある状態での最小値を示す点を求めるには
ラグランジュの未定乗数法
が有効です。
ラグランジュの未定乗数法
\(f(x, y)\)を最小にするにあたり
\(g(x, y) = 0\)
の拘束条件があるとき、
\(F(x, y) = f(x, y) + \lambda g(x, y)\)
として、
(x,y)が極値を与えるならば、
\(\displaystyle \frac{\partial F}{\partial x} = \displaystyle \frac{\partial F}{\partial y} = \displaystyle \frac{\partial F}{\partial \lambda} = 0 \)
を満たす。
近似平面は重心を通る
このラグランジュの未定乗数法に従い、
\(F(t, h) = f(t, h) – \lambda g(t, h)\)
\( = \displaystyle \sum_i (t \cdot p_i \ – h)^2 – \lambda (t \cdot t – 1)\)
とおきます。
まず、
\(\displaystyle \frac{\partial F}{\partial h} = 0\)
を考えます。
\(\displaystyle \frac{\partial F}{\partial h} = 2(t \cdot \displaystyle \sum_i p_i \ – N h) = 0\)
\(h = t \cdot \displaystyle \frac {1}{N}\displaystyle \sum_i p_i\)
となります。
ここで、
\(\displaystyle \frac {1}{N}\displaystyle \sum_i p_i\)
は点群の重心を表しますので、平面の式
\(t \cdot p = h\)
の式から、
「重心は近似平面上にある」
ことがわかります。
正方行列の固有ベクトル・固有値が値を与える
ここでいったん、式を簡略化するために
重心を
\(com = \displaystyle \frac {1}{N}\displaystyle \sum_i p_i\)
として
\(q_i = p_i – com\)
というように、平面を重心分ずらした式を考えます。
\(h = 0\)
となり、
\(f(t) = \displaystyle \sum_i (t \cdot q_i)^2\)
として
\(F(t,\lambda) = \displaystyle \sum_i (t \cdot q_i)^2 – \lambda(t \cdot t – 1)\)
について
\(\displaystyle \frac{\partial F}{\partial t} = 0 \)
を考えます。
\(\displaystyle \frac{\partial F}{\partial t} = 2 \displaystyle \sum_i q_i(t\cdot q_i) – 2\lambda t\) = 0
ここで
\(a (b \cdot c) = (a \cdot b^{\mathrm{T}}) \cdot c \)
の式より
\(\displaystyle \sum_i q_i \cdot q_i^{\mathrm{T}} t – \lambda t = 0\)
\(Q = \displaystyle \sum_i q_i \cdot q_i^{\mathrm{T}}\)
とおくと、
\(Q \cdot t – \lambda t = 0\)
となり、この式を満たす\(t\)と\(\lambda \)は、
\(Q\)の固有ベクトルと固有値
に他なりません。
そのため
\(t\)が行列\(Q\)の固有ベクトルのときに
\(\displaystyle \frac{\partial F}{\partial t} = 0 \)
となり、
\(f(t) = \displaystyle \sum_i (t \cdot q_i)^2\)
が極値をとることがわかります。
最小の固有値に対応する固有ベクトルが法線ベクトルとなる
極値のなかでどの固有値、固有ベクトルが最小値にあたるかを考えます。
もとの最小値にする目的の関数
\(f(t) = \displaystyle \sum_i (t \cdot q_i)^2\)
\(= t^{\mathrm{T}} \displaystyle \sum_i \cdot q_i \cdot q_i^{\mathrm{T}} \cdot t\)
に
固有ベクトルvを
\(t = v\)
として代入します。
\(Q = \displaystyle \sum_i q_i \cdot q_i^{\mathrm{T}}\)を代入し
\(f(t) = v \cdot (Q \cdot v\)
Qの固有ベクトルである\(v\)は\(\lambda\)を固有値として
\(Qv = \lambda v\)
を満たすので、
\(f(t) = v \cdot (\lambda v\)
\(= \lambda \|v\|^2 \)
\(= \lambda\) : 法線ベクトル\(\|v\|^2 = 1\)
となります。
つまり、
\(\displaystyle \frac{\partial F}{\partial t} = 0 \) のとき
\(Q =\) 固有値
ということです。
ですから、
複数ある固有値のなかで、
もっとも小さい固有値をとる固有ベクトル
が、近似平面の法線ベクトルとなります。
こっちの方が直感的にはわかりやすいですね。