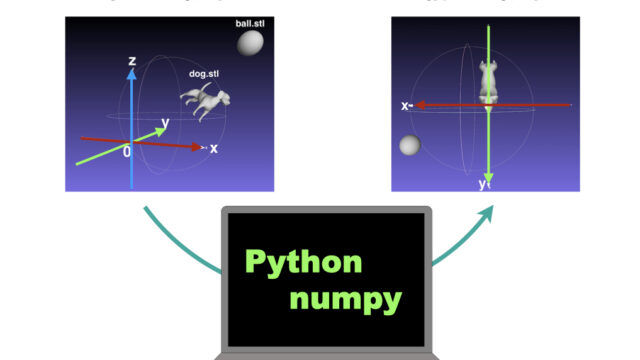
そんなときは点をまるごと使って計算できるよ。
点のかたまり同士をできるだけマッチさせるという手法があります。
ICP(Iterative Closest Point)
というアルゴリズムです。
1.2つの点群の間を最小距離にするICPアルゴリズム
ICPによって2つの点群どうしの距離がなるべく小さくなるように動かすことができます。
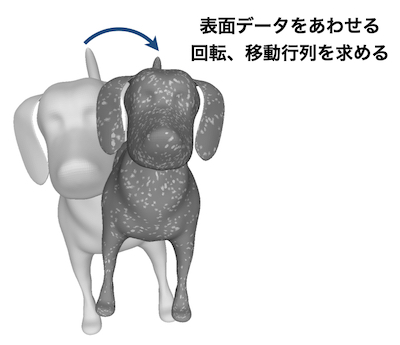
表面データは点の集合に面を貼ったものなので、全体がまとまって移動するなら同じアルゴリズムが使えます。
下の図のようなイメージです。
2匹の犬の表面データです。
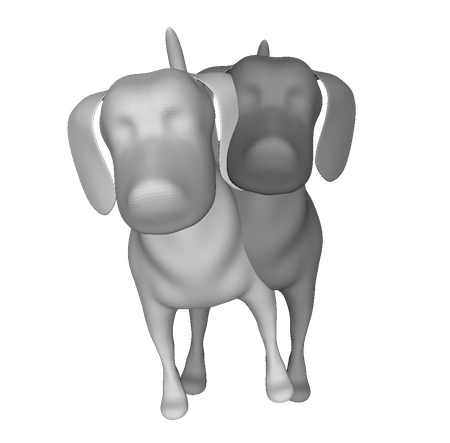
https://free3d.com/3d-model/dog-v2–703191.htmlよりダウンロード
実際の計算はイテレーションといって、ステップごとに近づけていきます。
この場合は15ステップ行っています。
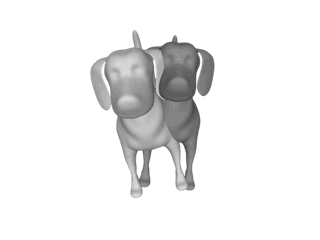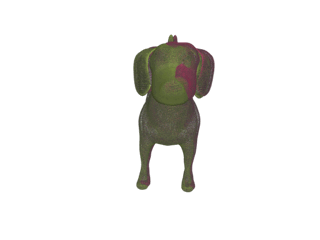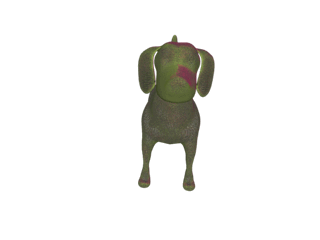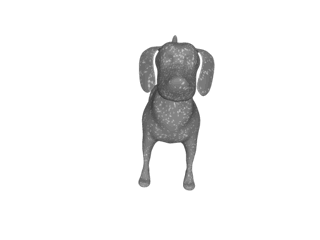
実際の計算を行う際は、
- 表面感距離が一定以下になったらストップする
- 最大20回(例)のイテレーションでストップする
というように終了条件を決めることができます。
2.ICPの注意点 -ローカルミニマムに注意-
このICPで気をつけないといけないのは、
距離が近い2つの面にしか用いることができない。
ということです。
最適化計算一般に言えることですが、
データが最小になるところ
この場合は2つの点群間の距離が最小になるところ
を目指すプログラムです。
これらは
ローカルミニマム(local minimum)
におちいってしまうというリスクがあります。
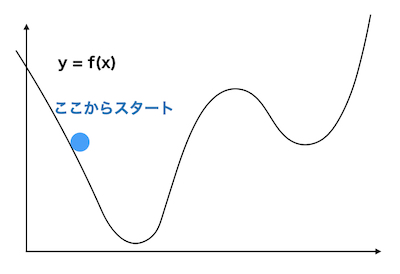
具体的には下のようなグラフを考えます。
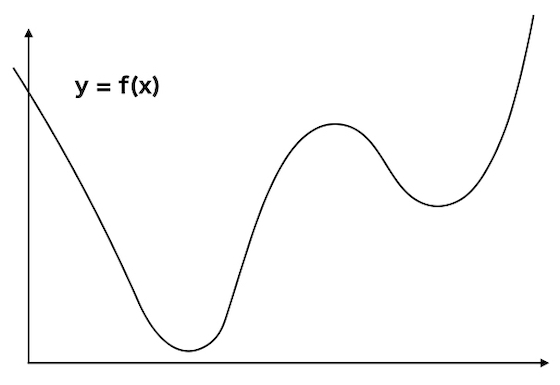
「ボールを斜面から転がして、止まったところが最小値」
というアルゴリズムを考えます。
すると、最小値から近い場所からスタートしていれば、ボールの止まった場所が最小値となります
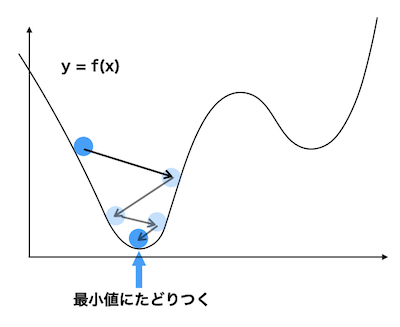
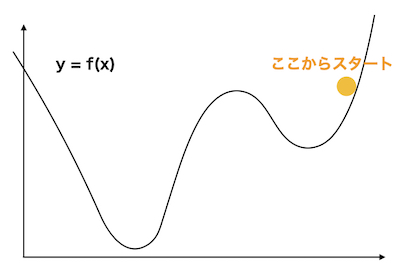
最小値から遠い場所からスタートしていると、
「その付近での最小値」
に収まって動かなくなってしまいます。
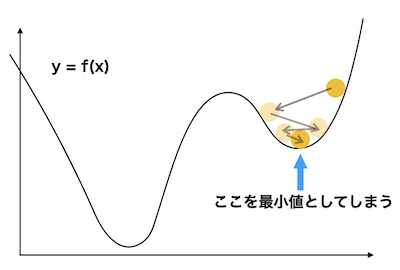
このように
ローカルミニマムに収束してしまうとアルゴリズムが進まなくなり、最小値にたどり着けなくなってしまうのです。
実際さきほどの犬の表面データでも離れてスタートすると下のようになってしまいます。

ICP前:さきほどより離れた位置より開始

ICP後:近づいてはいるが、表面間距離は最小にはなっていない
そのため、ICPを始める前にだいたいの位置をあわせてやる必要があります。
3.2つの表面データにICPを行うプログラムコード
Pythonを使ってICPを行うコードを書きます。
目標は、ICPアルゴリズムの結果出力される、
回転と移動の情報を行列で取得することです。
そのためにはvtk(the Visualization Toolkit)というライブラリを使います。
pip install vtk
でインストールできます。
vtkは可視化に大変有用なソフトですが、構造が非常に複雑のため理解にかなりの時間を要します。
「とりあえずICPが使えればいいや」
という使い方ができるようにスクリプトを組みました。
python, vtkを使用したicpのコード
必要なモジュール : numpy, numpy-stl, vtk
参考ページ:kitwareのvtk-pythonのexample
import numpy as np
import vtk
from stl import mesh
def main(source_stl, target_stl, max_iteration=20):
"""
入力
source_stl:もとのstlファイル, target_stl:出力先のstlファイル
max_iteration : ステップ数
出力
result_matrix (変換に必要な4x4行列)
加えてsource_stlにpostICPという名前をつけてICP後のstlを保存
"""
# stlをvtkで読み取れる点データvtk.polyDataに変換(stl2vtkpointsは下に定義)
source_vtk_data = stl2vtkpoints(source_stl)
target_vtk_data = stl2vtkpoints(target_stl)
# ============ run ICP ==============
icp = vtk.vtkIterativeClosestPointTransform()
#入力、出力データをセット
icp.SetSource(source_vtk_data)
icp.SetTarget(target_vtk_data)
#剛体に設定
icp.GetLandmarkTransform().SetModeToRigidBody()
icp.DebugOn()
icp.SetMaximumNumberOfIterations(max_iteration)
icp.StartByMatchingCentroidsOff()
icp.Modified()
icp.Update()
#icpの結果から4x4行列を出力
icpTransformFilter = vtk.vtkTransformPolyDataFilter()
transform_matrix = icpTransformFilter.GetTransform().GetMatrix()
result_matrix = np.identity(4)
for i in range(4):
for j in range(4):
result_matrix[i][j] = transform_matrix.GetElement(i, j)
#numpy-stlを使用して出力された変換行列で入力データを移動させる
source_mesh = mesh.Mesh.from_file(source_stl)
source_mesh.transform(result_matrix)
source_mesh.save(source_stl.replace('.stl','_postICP.stl'))
#---postICP.stlで保存
return result_matrix
#変換行列を返す
def stl2vtkpoints(stl_file):
# stlファイルをvtkのポイントデータに変換
stl_data = mesh.Mesh.from_file(stl_file)
stl_points =stl_data.points.reshape([-1, 3])
vtk_data = vtk.vtkPolyData()
vtk_data_points = vtk.vtkPoints()
vtk_data_vertices = vtk.vtkCellArray()
for point in stl_points:
id = vtk_data_points.InsertNextPoint(point)
vtk_data_vertices.InsertNextCell(1)
vtk_data_vertices.InsertCellPoint(id)
vtk_data.SetPoints(vtk_data_points)
vtk_data.SetVerts(vtk_data_vertices)
return vtk_data
このデータで先程のdog1.stlとdog2.stlの位置合わせを行います。

import icp_python
from stl import mesh
matrix = icp_python.main('dog1.stl', 'dog2.stl')
print(matrix)
#[[ 0.9730126 -0.11119069 -0.20219573 -2.19660497]
# [ 0.09364225 0.99112002 -0.09440468 -1.35194807]
# [ 0.21089716 0.07292288 0.97478441 0.53585268]
# [ 0. 0. 0. 1. ]]
numpy-stlの方が直感的にわかりやすいので、stlの保存や変換には私はnumpy-stlを使っています。