座標系をあわせる　絶対座標とローカル座標

２つのものの角度をみるときに、一方からみたときのもう一方の角度を計算する必要がある事があります。

私は整形外科ですが、例えば
膝の曲がっている角度をみたいときは
「大腿骨からみた下腿の骨の角度」
を測ります。

こういったときに必要なのが

ということです。

=> 座標変換のスクリプトはこちらのページ

ローカル座標系と絶対座標系

ここでは例として、

飛行機に乗っている人と
地上（管制塔）にいる人を考えます。
そして
両者から見た鳥の位置
を考えます。

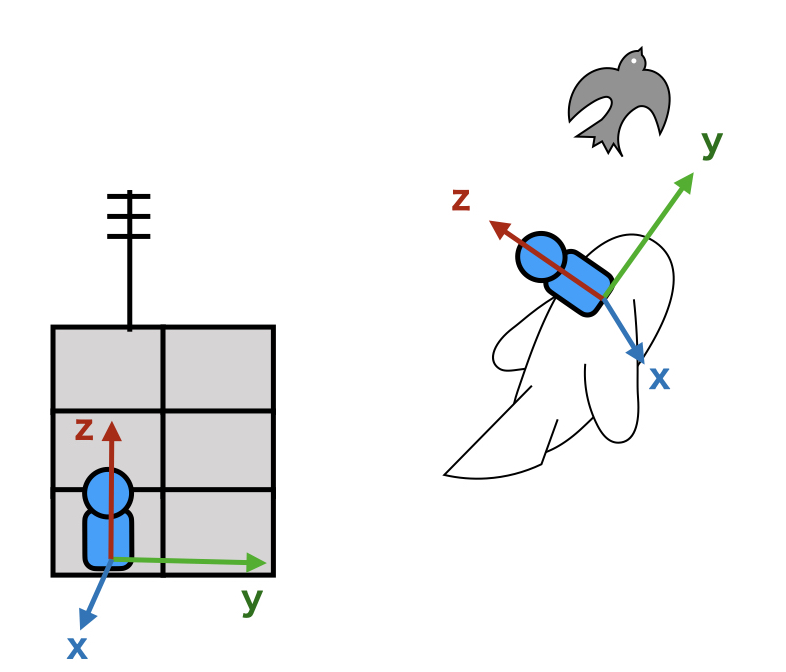
地上と飛行機の中にそれぞれ座標の軸があり、
この座標(x, y, z)の数値でものの位置を決めているとします。

基準となる座標系を絶対座標系
動いている座標をローカル座標系
とします。

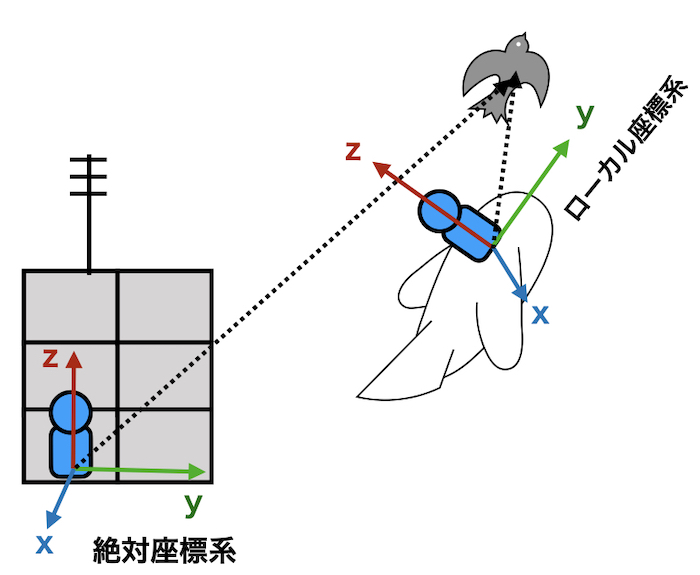
ここでは
地上　 ＝　絶対座標系
飛行機 ＝　ローカル座標系
です。

ローカル座標系の中での位置

ある時点の鳥の位置を考えます。

ローカル座標の中での鳥の位置が
\((x_L, y_L, z_L)\)
だったとします。

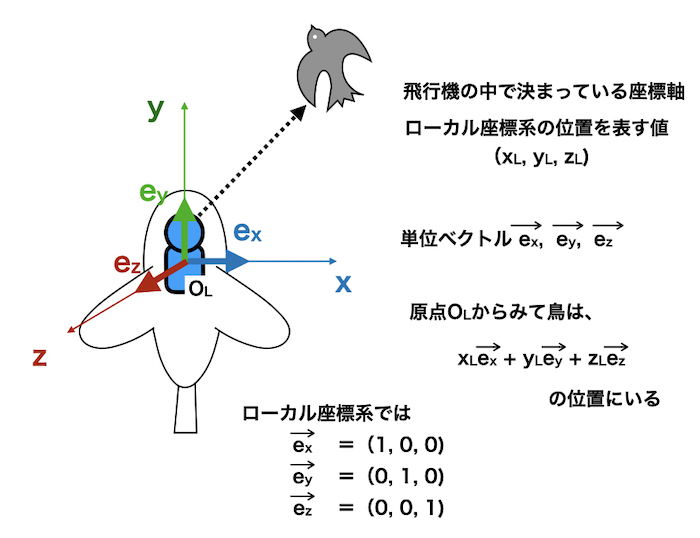
この鳥の位置はローカル座標の原点\(O_L\)からみると

\(x_L\overrightarrow{e_x} + y_L\overrightarrow{e_y} + z_L\overrightarrow{e_z}\)

という単位ベクトルの和で表せます。
当然ですが、
ローカル座標系におけるローカル座標の単位ベクトルは

\(\overrightarrow{e_x} = (1, 0, 0)\)
\(\overrightarrow{e_y} = (0, 1, 0)\)
\(\overrightarrow{e_z} = (0, 0, 1)\)
です。

絶対座標系での位置への変換

つぎに、絶対座標系での鳥の位置を考えます。

それぞれの座標系の中で、
長さ１の単位ベクトルがx,y,z方向に

\(\overrightarrow{e_x}, \overrightarrow{e_y}, \overrightarrow{e_z}\)

で定義されています。

絶対座標系から飛行機をみた時、
ローカル座標系のx, y, z軸は傾いているため、

 

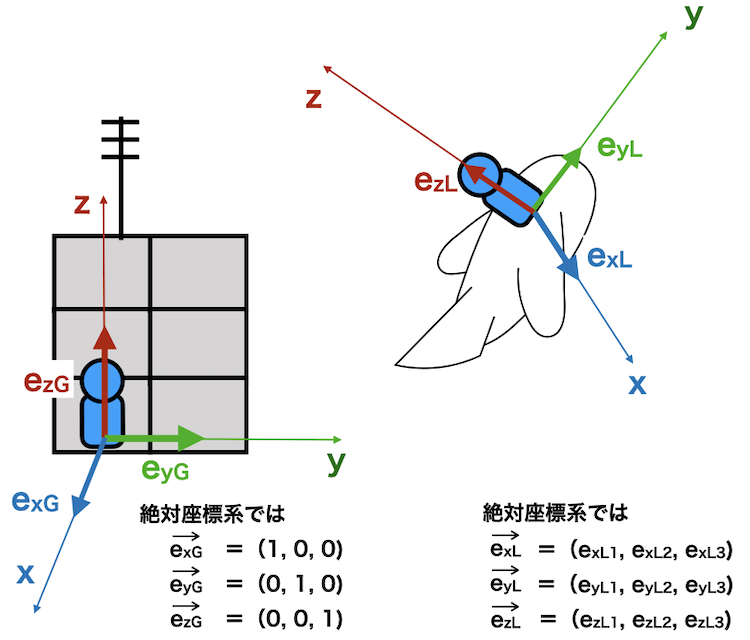
ローカル座標系の単位ベクトル\(\overrightarrow{e_{xL}}, \overrightarrow{e_{yL}}, \overrightarrow{e_{zL}}\)は
それぞれの

\(\overrightarrow{e_{xL}} = (e_{xL1}, e_{xL2}, e_{xL3})\)
\(\overrightarrow{e_{yL}} = (e_{yL1}, e_{yL2}, e_{yL3})\)
\(\overrightarrow{e_{zL}} = (e_{zL1}, e_{zL2}, e_{zL3})\)

のように、絶対座標系のx, y, zの成分を持っています。

ローカル座標\((x_L, y_L, z_L)\)の鳥の位置を
絶対座標で\((x_G, y_G, z_G)\)としてもとめると

 
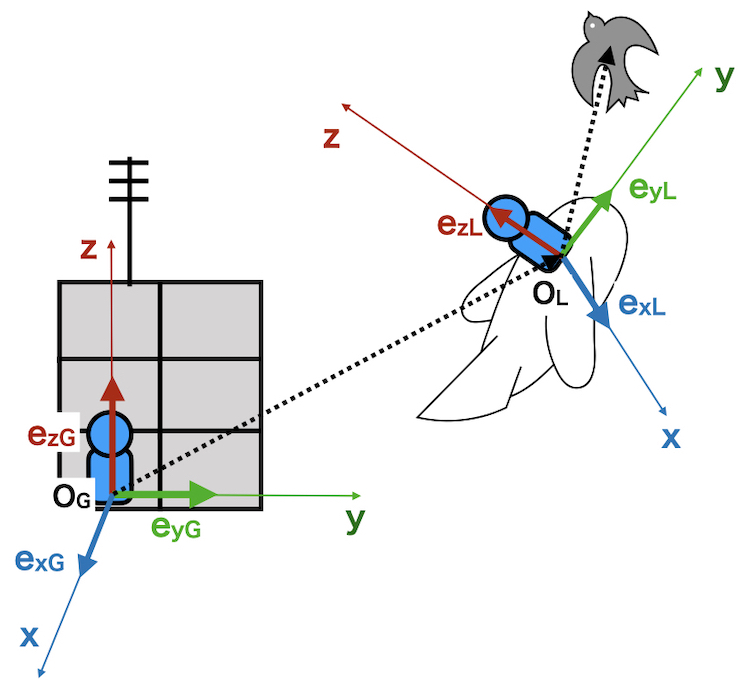
\(x_L\overrightarrow{e_{xL}} + y_L\overrightarrow{e_{yL}} + z_L\overrightarrow{e_{zL}} + \overrightarrow{O_GO_L} \)
となり、
成分で書くと

\(
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
=\begin{pmatrix}
e_{xL1} & e_{yL1} & e_{zL1} \\
e_{xL2} & e_{yL2} & e_{zL2} \\
e_{xL3} & e_{yL3} & e_{zL3}
\end{pmatrix}
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
+ \overrightarrow{O_GO_L}
\)

という、単位ベクトルからなる行列とローカル座標系での座標値の内積で書けます。

これを
\(
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
= M
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
+ t
\)

\(M = \left(
\begin{array}{c}
\overrightarrow{e_{xL}} \\
\overrightarrow{e_{yL}} \\
\overrightarrow{e_{zL}}
\end{array}
\right) ^{\mathrm{T}}
\hspace{10pt}
t = \overrightarrow{O_GO_L}
\)
 
※ \(T\)は転置行列

と書くと、回転移動する行列（回転行列）と移動成分に分けることができます。

import numpy as np
v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
v3 = np.array([7, 8, 9])

M = np.array([v1, v2, v3])
print(M)
# [[1 2 3]
#  [4 5 6]
#  [7 8 9]]

print(M.T)  #転置行列
# [[1 4 7]
#  [2 5 8]
#  [3 6 9]]

絶対座標系からローカル座標系への変換

絶対座標系で\((x_G, y_G, z_G)\)の位置にいる鳥を
ローカル座標系で表すには、逆の計算を行えばいいわけです。

\(
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
= M
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
+ t
\)

の式から計算します。

\(
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
– t
= M
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
\)
 
両辺に\(M^{-1}\)を左からかけます
 
\(
M^{-1}
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
– M^{-1}t
=
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
\)
 
ここでMは回転行列なので
\(M^{-1} = M^{\mathrm{T}}\)
ですから
 
\(
M^{\mathrm{T}}
\left(
\begin{array}{c}
x_G \\
y_G \\
z_G
\end{array}
\right)
– M^{\mathrm{T}}t
=
\left(
\begin{array}{c}
x_L \\
y_L \\
z_L
\end{array}
\right)
\)
 
となります。
回転行列は
 
\(M^{\mathrm{T}} = \left(
\begin{array}{c}
\overrightarrow{e_{xL}} \\
\overrightarrow{e_{yL}} \\
\overrightarrow{e_{zL}}
\end{array}
\right)
\hspace{10pt}
\)
 
移動行列は

\(
– M^{\mathrm{T}} \cdot \overrightarrow{O_GO_L}
\)

です。

回転と移動を一気に行う4×4行列

これら回転、移動の変換を4×4行列一つで表す方法があります。

ある複数の点を移動させる時、
回転　⇒　移動の手順に分解し
回転は3×3行列、移動はx, y, z成分の3×1ベクトルで表現されます。

回転行列を
\(Rot=
\begin{pmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{pmatrix}\)

移動行列を
\(t = \left(
\begin{array}{c}
t_x \\
t_y \\
t_z
\end{array}
\right)\)

とします。
 
もとの点piが

\(pi=\left(
\begin{array}{c}
p_{ix} \\
p_{iy} \\
p_{iz}
\end{array}
\right)\)

の時、

\(Rot \cdot p_i + t\)

が変換先の行列ですが、
変換元の行列に
 
\(pi=\left(
\begin{array}{c}
p_{ix} \\
p_{iy} \\
p_{iz} \\
1
\end{array}
\right)\)
 
と、1の成分を加えます。　
そして変換行列を4×4の形にして
 
\(R=
\left(
\begin{array}{ccc|c}
& & &\\
& \Large{Rot} & & \large{t}\\
& & & \\
\hline
& \large{0} & & \large{1}
\end{array}
\right)
\)
 
とすると
 

\(
R \cdot pi =
\begin{pmatrix}
r_{11} & r_{12} & r_{13} & t_x\\
r_{21} & r_{22} & r_{23} & t_y\\
r_{31} & r_{32} & r_{33} & t_z\\
0 & 0 & 0 & 1
\end{pmatrix}
\cdot
\left(
\begin{array}{c}
p_{ix} \\
p_{iy} \\
p_{iz} \\
1
\end{array}
\right)
=
\left(
\begin{array}{c}
\\
Rot \cdot pi + t \\
\\
1
\end{array}
\right)\)

となり、１回の内積で変換先の座標が得られます。
 

  

となります。

注意事項　4×4変換行列は 逆行列=逆変換ではない！

3×3回転行列は上の式をみても分かる通り、

\(^{L}Rot_G = (^{G}Rot_L) ^{-1}\)

という

逆行列 = 逆変換

の関係が成り立ちます。

しかし、4×4変換行列の変換行列は

回転　⇒　移動

を含むため、この逆変換は

移動　⇒　回転となります。

そのため、4×4変換行列

\(\left(
\begin{array}{ccc|c}
& & &\\
& \Large{Rot} & & \large{t}\\
& & & \\
\hline
& \large{0} & & \large{1}
\end{array}
\right)\)

の逆変換は

\(\left(
\begin{array}{ccc|c}
& & &\\
& \Large{Rot^{-1}} & & – Rot^{-1} \cdot {t}\\
& & & \\
\hline
& \large{0} & & \large{1}
\end{array}
\right)\)

となります。