Pythonによる座標変換のプログラム

ここでは、実際に座標系をあわせる作業をPythonのスクリプトを使って行います。

座標系の式についての説明はこちら

座標系の定義の例

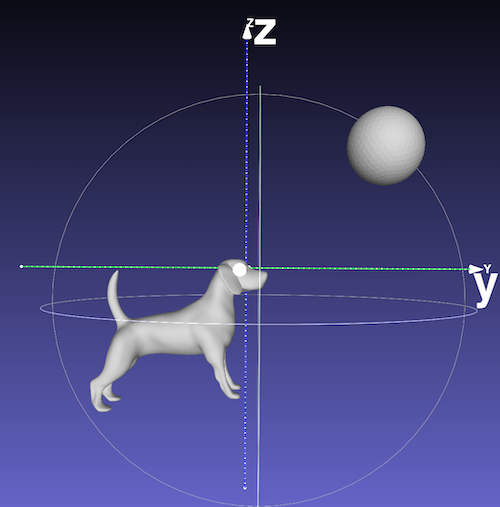
例として、以下のような犬の表面データモデルを考えます。

あわせボールの表面データもおいておきます。

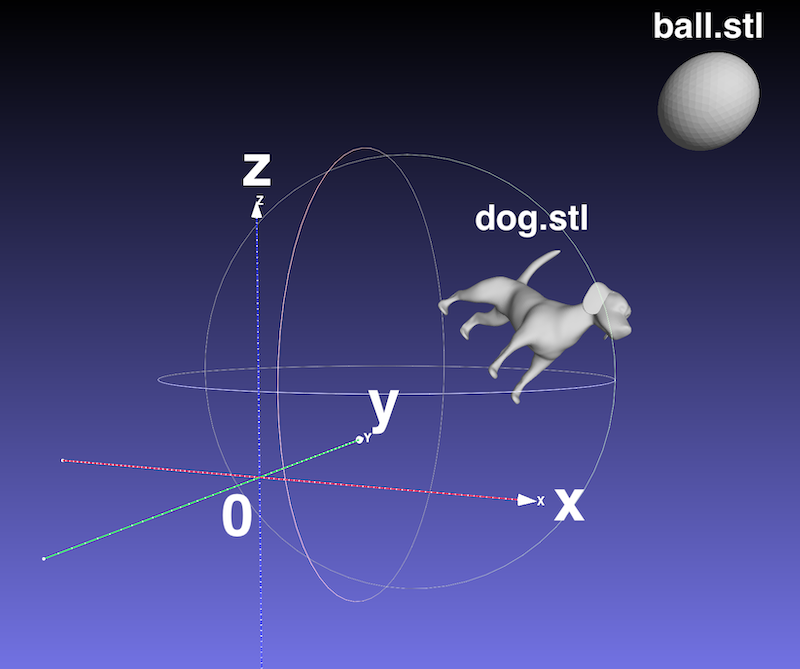
犬のデータはfree3d.comよりダウンロード

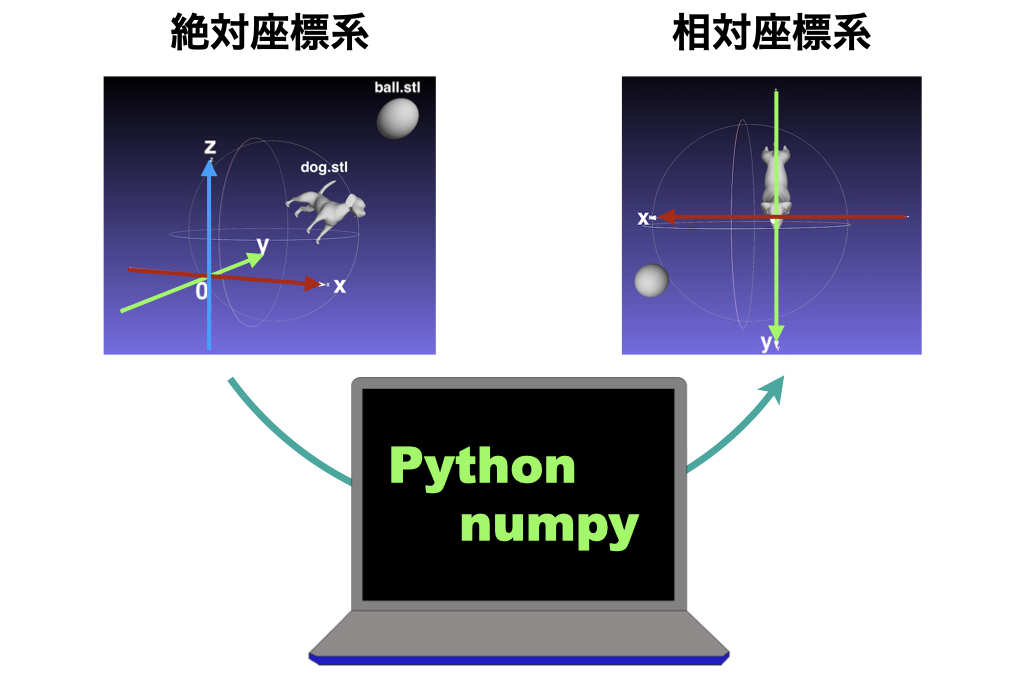
表示されているx, y, z軸はあらかじめ決まっている絶対座標での軸です。

この軸からだけでは、犬からボールの方向、位置は正確に表せません。

そのため、絶対座標を犬からみた座標に合わせます。

ここでは例として
参照点として、犬の
右目、左目、鼻、しっぽを使います。

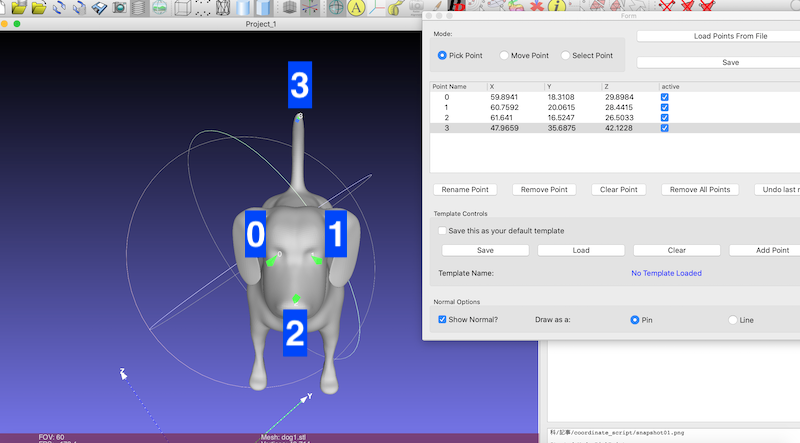
Meshlab上で点データを右目、左目、鼻、しっぽの順に点をとります。

「dog.pp」
として保存します。

犬のローカル座標として、

とします。

「犬のしっぽから鼻にむかう直線」をy軸にしたいところですが、
そうなるとx軸とy軸が直交していることが確約されなくなってしまうため、このような軸のとり方をします。

スクリプト

前ページの座標変換の式

使用してスクリプト

“dog_axis.py”
を書きます。

import numpy as np

def main(right_eye, left_eye, nose, tail):
    origin = (right_eye + left_eye) / 2
    #原点を両目の中点とする
    px = right_eye - left_eye
    # x軸は左目→右目
    py = nose - tail
    # 「しっぽから鼻にむかう直線」

    """それぞれの単位ベクトルを計算"""
    ex = px / np.linalg.norm(px)
    ez = np.cross(px, py) / np.linalg.norm(np.cross(px, py))
    ey = np.cross(ez, ex)

    """変換行列 4x4 を作成"""
    #ローカル座標（犬から見た座標）を絶対座標に変換する行列
    R_LtoG = np.identity(4)

    R_LtoG[:3, :3] = np.array([ex, ey, ez]).T
    #回転行列を代入
    R_LtoG[:3, 3] = origin
    #移動ベクトルを代入

    #絶対座標からローカル座標（犬からみた座標）に変換する行列
    R_GtoL = np.identity(4)
    R_GtoL[:3, :3] = np.array([ex, ey, ez])
    R_GtoL[:3, 3] = - np.dot(np.array([ex, ey, ez]), origin) 

    return (R_GtoL, R_LtoG)

外から呼び出します。
Meshlabで読み取った点を使用するため、
Meshlabの.ppファイルを読み取れるスクリプトを使います。

=> Meshlabでとった点を読み取るスクリプト

from stl import mesh

import dog_axis
import point_class    #Meshlabのポイントを読み込むモジュール

"""Meshlabの点を読み込む"""
dog_points = point_class.MeshlabPp('dog.pp')    
right_eye = dog_points.point_list[0]
left_eye = dog_points.point_list[1]
nose = dog_points.point_list[2]
tail = dog_points.point_list[3]

R_GtoL, R_LtoG = dog_axis.main(right_eye, left_eye, nose, tail)
print(R_GtoL)
#[[ -0.35505373  -0.71856705   0.59799519  17.76227135]
# [  0.47873701  -0.68918876  -0.54390232   0.20790221]
# [  0.80296185   0.09316788   0.58870368 -67.40000847]
# [  0.           0.           0.           1.        ]]
print(R_LtoG)
#[[-0.35505373  0.47873701  0.80296185 60.3266655 ]
# [-0.71856705 -0.68918876  0.09316788 19.1861825 ]
# [ 0.59799519 -0.54390232  0.58870368 29.1699585 ]
# [ 0.          0.          0.          1.        ]]

"""numpy.stlを使って犬のローカル座標に表面データを移動"""
dog_stl = mesh.Mesh.from_file('dog.stl')
ball_stl = mesh.Mesh.from_file('ball.stl')

dog_stl.transform(R_GtoL)
ball_stl.transform(R_GtoL)

dog_stl.save('dog_local.stl')
ball_stl.save('ball_local.stl')

犬を中心とした座標系に犬の表面データとボールの表面データが移動されます。
この座標系でいろいろ計測すれば、犬からの位置関係としての値が計算できるというわけです。

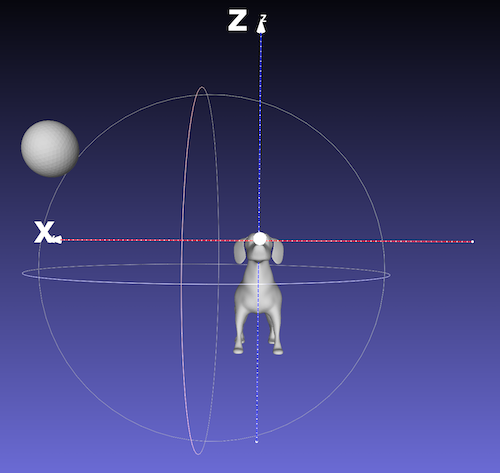
正確な位置が出したければ、ローカル犬座標でのボールの座標を求めます。

numpy-stlには重心を出す方法がありますので、

from stl import mesh

ball_local = mesh.Mesh.from_file('ball_local.stl')
volume, cog, inertia = ball_local.get_mass_properties()
# cog : center of gravity(重心)
print(cog)
#[37.40975436 18.7481968  16.09440369]

と客観的に表すことができます。

「右上の前にあります。」でもわかるのですが、このように定量化が求められるときにこの方法は役に立ちます。