ここでは回転行列とオイラー角の計算をスクリプトにしていきます。
オイラー角の原理についてはこちらの記事参照
⇒ オイラー角と回転角度の原理
このページの内容
回転角度から回転行列を計算するスクリプト
回転行列3×3行列を入力すると、オイラー角を出力するスクリプトを書きます。
euler.py
import numpy as np
def rotation_matrix(theta1, theta2, theta3, order='xyz'):
"""
入力
theta1, theta2, theta3 = 回転角度 回転順にtheta 1, 2, 3
oreder = 回転順 たとえば X, Z, Y順なら'xzy'
出力
3x3回転行列
"""
c1 = np.cos(theta1 * np.pi / 180)
s1 = np.sin(theta1 * np.pi / 180)
c2 = np.cos(theta2 * np.pi / 180)
s2 = np.sin(theta2 * np.pi / 180)
c3 = np.cos(theta3 * np.pi / 180)
s3 = np.sin(theta3 * np.pi / 180)
if order == 'xzx':
matrix=np.array([[c2, -c3*s2, s2*s3],
[c1*s2, c1*c2*c3-s1*s3, -c3*s1-c1*c2*s3],
[s1*s2, c1*s3+c2*c3*s1, c1*c3-c2*s1*s3]])
elif order=='xyx':
matrix=np.array([[c2, s2*s3, c3*s2],
[s1*s2, c1*c3-c2*s1*s3, -c1*s3-c2*c3*s1],
[-c1*s2, c3*s1+c1*c2*s3, c1*c2*c3-s1*s3]])
elif order=='yxy':
matrix=np.array([[c1*c3-c2*s1*s3, s1*s2, c1*s3+c2*c3*s1],
[s2*s3, c2, -c3*s2],
[-c3*s1-c1*c2*s3, c1*s2, c1*c2*c3-s1*s3]])
elif order=='yzy':
matrix=np.array([[c1*c2*c3-s1*s3, -c1*s2, c3*s1+c1*c2*s3],
[c3*s2, c2, s2*s3],
[-c1*s3-c2*c3*s1, s1*s2, c1*c3-c2*s1*s3]])
elif order=='zyz':
matrix=np.array([[c1*c2*c3-s1*s3, -c3*s1-c1*c2*s3, c1*s2],
[c1*s3+c2*c3*s1, c1*c3-c2*s1*s3, s1*s2],
[-c3*s2, s2*s3, c2]])
elif order=='zxz':
matrix=np.array([[c1*c3-c2*s1*s3, -c1*s3-c2*c3*s1, s1*s2],
[c3*s1+c1*c2*s3, c1*c2*c3-s1*s3, -c1*s2],
[s2*s3, c3*s2, c2]])
elif order=='xyz':
matrix=np.array([[c2*c3, -c2*s3, s2],
[c1*s3+c3*s1*s2, c1*c3-s1*s2*s3, -c2*s1],
[s1*s3-c1*c3*s2, c3*s1+c1*s2*s3, c1*c2]])
elif order=='xzy':
matrix=np.array([[c2*c3, -s2, c2*s3],
[s1*s3+c1*c3*s2, c1*c2, c1*s2*s3-c3*s1],
[c3*s1*s2-c1*s3, c2*s1, c1*c3+s1*s2*s3]])
elif order=='yxz':
matrix=np.array([[c1*c3+s1*s2*s3, c3*s1*s2-c1*s3, c2*s1],
[c2*s3, c2*c3, -s2],
[c1*s2*s3-c3*s1, c1*c3*s2+s1*s3, c1*c2]])
elif order=='yzx':
matrix=np.array([[c1*c2, s1*s3-c1*c3*s2, c3*s1+c1*s2*s3],
[s2, c2*c3, -c2*s3],
[-c2*s1, c1*s3+c3*s1*s2, c1*c3-s1*s2*s3]])
elif order=='zyx':
matrix=np.array([[c1*c2, c1*s2*s3-c3*s1, s1*s3+c1*c3*s2],
[c2*s1, c1*c3+s1*s2*s3, c3*s1*s2-c1*s3],
[-s2, c2*s3, c2*c3]])
elif order=='zxy':
matrix=np.array([[c1*c3-s1*s2*s3, -c2*s1, c1*s3+c3*s1*s2],
[c3*s1+c1*s2*s3, c1*c2, s1*s3-c1*c3*s2],
[-c2*s3, s2, c2*c3]])
return matrix回転行列から回転角度を計算するスクリプト
回転角度も同様に計算の書き下しになります。
euler.pyの続き
import numpy as npは上に記載済み
def rotation_angles(matrix, order):
"""
入力
matrix = 3x3回転行列
oreder = 回転順 たとえば X, Z, Y順なら'xzy'
出力
theta1, theta2, theta3 = 回転角度 回転順にtheta 1, 2, 3
"""
r11, r12, r13 = matrix[0]
r21, r22, r23 = matrix[1]
r31, r32, r33 = matrix[2]
if order == 'xzx':
theta1 = np.arctan(r31 / r21)
theta2 = np.arctan(r21 / (r11 * np.cos(theta1)))
theta3 = np.arctan(-r13 / r12)
elif order == 'xyx':
theta1 = np.arctan(-r21 / r31)
theta2 = np.arctan(-r31 / (r11 *np.cos(theta1)))
theta3 = np.arctan(r12 / r13)
elif order == 'yxy':
theta1 = np.arctan(r12 / r32)
theta2 = np.arctan(r32 / (r22 *np.cos(theta1)))
theta3 = np.arctan(-r21 / r23)
elif order == 'yzy':
theta1 = np.arctan(-r32 / r12)
theta2 = np.arctan(-r12 / (r22 *np.cos(theta1)))
theta3 = np.arctan(r23 / r21)
elif order == 'zyz':
theta1 = np.arctan(r23 / r13)
theta2 = np.arctan(r13 / (r33 *np.cos(theta1)))
theta3 = np.arctan(-r32 / r31)
elif order == 'zxz':
theta1 = np.arctan(-r13 / r23)
theta2 = np.arctan(-r23 / (r33 *np.cos(theta1)))
theta3 = np.arctan(r31 / r32)
elif order == 'xzy':
theta1 = np.arctan(r32 / r22)
theta2 = np.arctan(-r12 * np.cos(theta1) / r22)
theta3 = np.arctan(r13 / r11)
elif order == 'xyz':
theta1 = np.arctan(-r23 / r33)
theta2 = np.arctan(r13 * np.cos(theta1) / r33)
theta3 = np.arctan(-r12 / r11)
elif order == 'yxz':
theta1 = np.arctan(r13 / r33)
theta2 = np.arctan(-r23 * np.cos(theta1) / r33)
theta3 = np.arctan(r21 / r22)
elif order == 'yzx':
theta1 = np.arctan(-r31 / r11)
theta2 = np.arctan(r21 * np.cos(theta1) / r11)
theta3 = np.arctan(-r23 / r22)
elif order == 'zyx':
theta1 = np.arctan(r21 / r11)
theta2 = np.arctan(-r31 * np.cos(theta1) / r11)
theta3 = np.arctan(r32 / r33)
elif order == 'zxy':
theta1 = np.arctan(-r12 / r22)
theta2 = np.arctan(r32 * np.cos(theta1) / r22)
theta3 = np.arctan(-r31 / r33)
theta1 = theta1 * 180 / np.pi
theta2 = theta2 * 180 / np.pi
theta3 = theta3 * 180 / np.pi
return (theta1, theta2, theta3)実際に計算してみる
回転行列の計算と回転角度の逆算
pythonのインタープリタ内で実行してみます
import euler
rotation_mat = euler.rotation_matrix(10, 20, 30, 'yzx')
#yzx周りに10, 20, 30°回転させる回転行列を計算
print(rotation_mat)
# [[ 0.92541658 -0.20487413 0.31879578]
# [ 0.34202014 0.81379768 -0.46984631]
# [-0.16317591 0.54383814 0.82317294]]
angles = euler.rotation_angles(rotation_mat, 'yzx')
#先程の回転行列からYZXのオイラー角を計算
print(angles)
# (10.0, 20.0, 29.999999999999993)
無事に回転行列から角度が計算されていることがわかります。
stlモデルを回転させる
具体例として飛行機のモデル airplane.stl を回転させて
正しく飛行機の軸（ローカル軸）で回転できているか確認します。
stlの回転には
「numpy-stl」を使用します。
pip install numpy-stl
でインストールできます。(numpy-stlの使用方法はこちらの記事を参照 ⬇）
numpy-stlまとめ PythonでSTLデータを操作する！表面データを移動、回転するときに行列計算を用いますが、PythonのNumpy-stlはこの計算を簡便にできるようにしたツールです。ここではNumpy-stlをもちいた表面データの計算を紹介します。...
numpy-stlを用いてモデルを回転させます。
import numpy as np
from stl import mesh
#stlの読み書きと移動に numpy-stlを使用する
#オリジナルモデルの読み込み
airplane = mesh.Mesh.from_file('airplane.stl')
#4x4行列を作成し、回転成分に3x3回転行列を入れる
rotation_x = np.identity(4)
rotation_x[:3, :3] = euler.rotation_matrix(30, 0, 0, 'xzy')
#行列での回転と保存
airplane.transform(rotation_x)
airplane.save('airplane_x.stl')
#x軸まわりのみ回転したモデル
#同様にZ軸、y軸回りに回転する
airplane = mesh.Mesh.from_file('airplane.stl')
# stlは回転後のデータのため、読み直す
rotation_xz = np.identity(4)
rotation_xz[:3, :3] = euler.rotation_matrix(30, 60, 0, 'xzy')
airplane.transform(rotation_xz)
airplane.save('airplane_xz.stl')
#x軸, z軸まわりに回転したモデル
airplane = mesh.Mesh.from_file('airplane.stl')
rotation_xzy = np.identity(4)
rotation_xzy[:3, :3] = euler.rotation_matrix(30, 60, 90, 'xzy')
airplane.transform(rotation_xzy)
airplane.save('airplane_xzy.stl')
#x軸, z軸, y軸まわりに回転したモデル
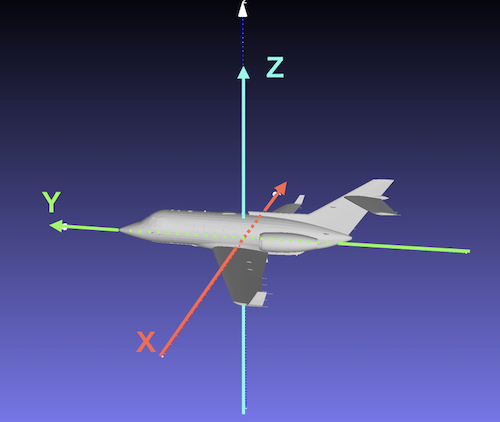
飛行機の座標軸
グレー：スタート地点(airplane.stl)
緑：X軸まわり回転したモデル(airplane_x.stl)
緑：X軸まわりに回転したモデル(airplane_x.stl)
オレンジ：X, Z軸まわりに回転したモデル(airplane_xz.stl)
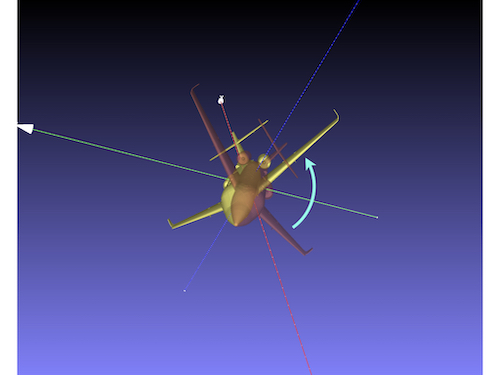
オレンジ：X, Z軸まわりに回転したモデル(airplane_xz.stl)
黄色：X, Z, Y軸回りに回転したモデル(airplane_xzy.stl)
オンラインコース
データキャンプ Data Scientist with Python Track
データサイエンスに特化したPythonのオンラインコース。numpy, matplotlib, pandas, scikit-learnなど統計解析、データ解析の授業が豊富。
それぞれの単元につき始めのchapterは無料体験で受講できる。 Web上入力なので環境設定は不要。
単一軸回転から計算する方法
回転行列の計算に、
ローカル軸回りに絶対座標を\(-\theta_1, -\theta_2, -\theta_3\)回転させて、最後に逆行列を求めるという計算過程から記載することもできます。
=> ローカル軸回りの単一軸回転で理解する方法はこちらに記載
euler.py続き
import numpy as npは上に記載済み
def axis_rotation(theta, axis_name):
#x,y,zのどれか単一軸回りに\(\theta\)回転させる回転行列を求める関数
"""
入力
theta = 回転角度
axis_name = 'x', 'y', 'z'のどれかを指定し、その軸回りの回転行列を求める。
出力
単軸周りの3x3回転行列
"""
c = np.cos(theta * np.pi / 180)
s = np.sin(theta * np.pi / 180)
if axis_name =='x':
rotation_matrix = np.array([[1, 0, 0],
[0, c, -s],
[0, s, c]])
if axis_name =='y':
rotation_matrix = np.array([[c, 0, s],
[0, 1, 0],
[-s, 0, c]])
elif axis_name =='z':
rotation_matrix = np.array([[c, -s, 0],
[s, c, 0],
[0, 0, 1]])
return rotation_matrix
def confirm_matrix(theta1, theta2, theta3, order='xyz'):
#オイラー角を求める関数
"""
入力
theta1, theta2, theta3 = 回転角度 回転順にtheta 1, 2, 3
order = 回転順 たとえば X, Z, Y順なら'xzy'
出力
3x3回転行列
"""
axis_name1 = order[0]
axis_name2 = order[1]
axis_name3 = order[2]
rotation1 = axis_rotation(-theta1, axis_name1)
rotation2 = axis_rotation(-theta2, axis_name2)
rotation3 = axis_rotation(-theta3, axis_name3)
#ローカル座標を中心に絶対座標を逆回転させる行列
matrix_local = np.dot(rotation3, np.dot(rotation2, rotation1))
#絶対座標で同じ相対位置にローカル座標をもっていく行列
matrix_global = matrix_local.T
return matrix_globalpythonインタープリタ内で
print(euler.rotation_matrix(30, 60, 90, ‘xzy’))
# [[ 3.06161700e-17 -8.66025404e-01 5.00000000e-01]
# [ 5.00000000e-01 4.33012702e-01 7.50000000e-01]
# [-8.66025404e-01 2.50000000e-01 4.33012702e-01]]
print(euler.confirm_matrix(30, 60, 90, ‘xzy’))
# [[ 3.06161700e-17 -8.66025404e-01 5.00000000e-01]
# [ 5.00000000e-01 4.33012702e-01 7.50000000e-01]
# [-8.66025404e-01 2.50000000e-01 4.33012702e-01]]
同じ回転行列が出力されるのがわかります。
回転行列は、
画像でイメージして納得できる部分と、
計算式から納得できる部分があります。
理解するには式を書き下しながら、実際のデータを回転させてみるとよいと思います。
画像でイメージして納得できる部分と、
計算式から納得できる部分があります。
理解するには式を書き下しながら、実際のデータを回転させてみるとよいと思います。
