整形外科であつかう骨には球の形状が多く見られます。
- 肩関節の上腕骨頭
- 股関節の大腿骨頭
などは代表的な球の形状をしている骨です。
計測や形状評価をするにあたって、これらの球の中心や半径を求めることがあります。
ここではその方法を記載します。
計算原理は式の変換がやや難しめなので、
「球面近似のPythonスクリプト」
からでもわかるようにしてあります。
=>球近似のPythonスクリプトはこちら
球面近似計算の原理
点群から球の半径と中心を近似する方法は
「最小二乗法」
で求めることができます。
半径を\(r\)とし、中心位置のベクトルを\(m\)とします。 そして点群のベクトルを\(v_k\)とします。
ここで
\(C = \displaystyle \sum_{k=1}^{n}\left\lbrace (v_k – m)^2 – r^2 \right\rbrace ^2 \)
を最小とする\(r\)と\(m\)を考えます。
\(r\)と\(m\)に対して偏微分をし、0になる値を求めます。
\(r\)に対して偏微分をすると、
\(-4r \displaystyle \sum_{k=1}^{n}\left\lbrace (v_k – m)^2 – r^2 \right\rbrace = 0 \)
半径\(r\)は0ではないとして、
\(r = \sqrt{\displaystyle \frac{1}{N}\sum_{k=1}^{n}(v_k – m)^2}\) ・・・式①
となります。
\(m\)による偏微分は
\(\displaystyle \sum_{k=1}^{n}(v_k – m)\left\lbrace (v_k – m)^2 – r^2 \right\rbrace = 0\)
ここに上のrを代入して展開して整理をすると
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k^3 – \displaystyle\frac{1}{N}\sum_{k=1}^{n}v_k \cdot \displaystyle\frac{1}{N}\sum_{k=1}^{n}v_k^2 – 2 \left\lbrace \displaystyle \frac{1}{N}\sum_{k=1}^{n} v_k(v_k \cdot m) – \displaystyle\frac{1}{N}\sum_{k=1}^{n}v_k (m \cdot \displaystyle\frac{1}{N}\sum_{k=1}^{n}v_k)\right\rbrace \) = 0
乗数平均でこみいっているので、
3乗平均、2乗平均、1乗平均を書き換えるとスッキリします。
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k^3 = \overline{v_k^3}\)
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k^2 = \overline{v_k^2}\)
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k = \overline{v_k}\)
とすると
\(\overline{v_k^3} – \overline{v_k}(\overline{v_k^2}) = 2\left\lbrace \displaystyle \frac{1}{N}\sum_{k=1}^{n} v_k(v_k \cdot m) – \overline{v_k} (m \cdot \overline{v_k})\right\rbrace \)
ここで
\(a (b \cdot c) = (a \cdot b^{\mathrm{T}}) \cdot c \)
※ ベクトルは縦行列なので
\( (a \cdot b^{\mathrm{T}})\) は3×3行列
例えば
\(
a =
\left(
\begin{array}{c}
a_1 \\
a_2 \\
a_3
\end{array}
\right)
\) \(
b =
\left(
\begin{array}{c}
b_1 \\
b_2 \\
b_3
\end{array}
\right)
\)
であれば
\(a \cdot b^{\mathrm{T}} =
\left(
\begin{array}{ccc}
a_1b_1 & a_1b_2 & a_1b_3\\
a_2b_1 & a_2b_2 & a_2b_3 \\
a_3b_1 & a_3b_2 & a_3b_3
\end{array}
\right)
\)
です。
これを利用すると
\( A = 2\left( \displaystyle \frac{1}{N}\sum_{k=1}^{n} v_k \cdot v_k^{\mathrm{T}} – \overline{v_k} \cdot \overline{v_k}^{\mathrm{T}}\right) \) ・・・式②
\(b = \overline{v_k^3} – (\overline{v_k^2})\overline{v_k}\) ・・・・・・式③
として
\(A \cdot m = b\)
と表記できます。
ここから
\(m = A^{-1} \cdot b\)
以上で
半径 \(r\)
中心 \(m\)
が求まります。
球近似のPythonスクリプト
点群ベクトル\(v\)に対して
半径 \(r\)を
\(r = \sqrt{\displaystyle \frac{1}{N}\sum_{k=1}^{n}(v_k – m)^2}\) ・・・式①
より求め、
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k^3 = \overline{v_k^3}\)
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k^2 = \overline{v_k^2}\)
\(\displaystyle \frac{1}{N}\sum_{k=1}^{n}v_k = \overline{v_k}\)
として
\( A = 2\left( \displaystyle \frac{1}{N}\sum_{k=1}^{n} v_k \cdot v_k^{\mathrm{T}} – \overline{v_k} \cdot \overline{v_k}^{\mathrm{T}}\right) \) ・・・式②
\(b = \overline{v_k^3} – (\overline{v_k^2})\overline{v_k}\) ・・・・・・式③
\(A \cdot m = b\)
より
中心 \(m\)を求めます
計算をスクリプトに書いていきます。
ファイル名は
「fitting.py」
とします。
def sphere_fit(point_cloud):
"""
入力
point_cloud: 点群のxyz座標のリスト numpyのarray形式で3x3xN行列
出力
radius : 近似球の半径 スカラー
sphere_center : 球の中心座標 xyz numpyのarray
"""
A_1 = np.zeros((3,3))
#Aのカッコの中の1項目用に変数A_1をおく
v_1 = np.array([0.0,0.0,0.0])
v_2 = 0.0
v_3 = np.array([0.0,0.0,0.0])
#ベクトルの1乗、2乗、3乗平均の変数をv_1, v_2, v_3とする
#1乗、3乗はベクトル、2乗はスカラーとなる
N = len(point_cloud)
#Nは点群の数
"""シグマの計算"""
for v in point_cloud:
v_1 += v
v_2 += np.dot(v, v)
v_3 += np.dot(v, v) * v
A_1 += np.dot(np.array([v]).T, np.array([v]))
v_1 /= N
v_2 /= N
v_3 /= N
A = 2 * (A_1 / N - np.dot(np.array([v_1]).T, np.array([v_1])))
# 式②
b = v_3 - v_2 * v_1
# 式③
sphere_center = np.dot(np.linalg.inv(A), b)
# 式①
radius = (sum(np.linalg.norm(np.array(point_cloud) - sphere_center, axis=1))
/len(point_cloud))
return(radius, sphere_center)
スクリプトでの計算例(上腕骨)
上腕骨のstl表面データを使用して、上腕骨頭の球の近似をしてみます。
Meshlabで頭の丸い部分だけ抽出し、
sphere.stl
として保存します。
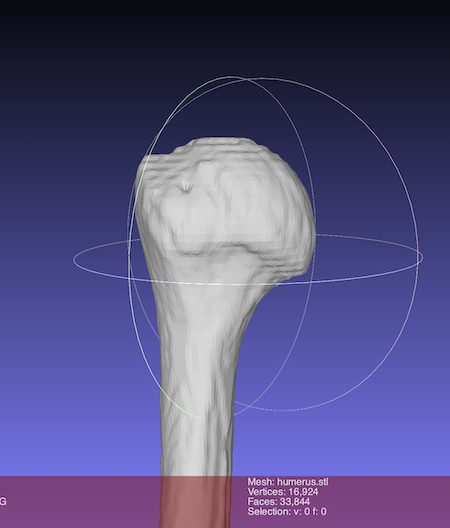
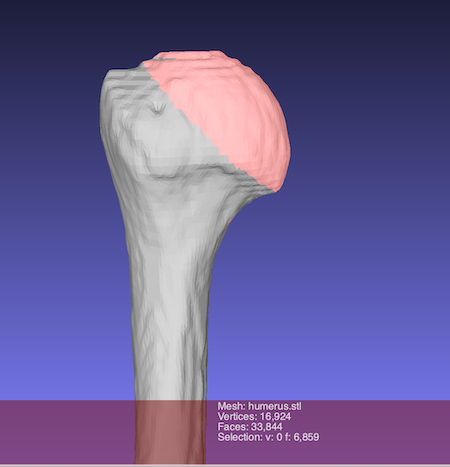

この部分の球近似を
外部でpythonインタープリタで試してみます。
import numpy as np
import fitting
from stl import mesh
# numpy-stlを使用します。
sphere_stl = mesh.Mesh.from_file('sphere.stl')
#stlファイルの読み込み
sphere_points = sphere_stl.points.reshape([-1, 3])
#stlから点群を抽出
print(sphere_points)
# [[ 154.80566 -124.725586 192.21085 ]
# [ 153.9873 -124.725586 192.33838 ]
# [ 153.9873 -124.098175 193.5 ]
# ...
# [ 157.29794 -124.725586 235.5 ]
# [ 157.26074 -124.711945 235.5 ]
# [ 157.26074 -124.725586 235.52 ]]
# 表面データの点群が代入されている
radius, center = fitting.sphere_fit(sphere_points)
# fitting.pyのsphere_fit関数で半径、中心を計算
print(radius)
# 23.087794980492543
print(center)
# [ 154.15674832 -133.40106545 213.64071843]
半径と中心が計算できました。
この球を先ほどの表面データと一緒に描画して結果を確認していきます。
半径と中心を指定して描画する
近似した球を確認する
fitting.pyに以下のスクリプトを追加して、計算結果の球を書き出してMeshlabで確認します。
"""半径と中心を定めて 点群ファイルに保存する"""
def draw_sphere(radius, sphere_center):
"""
入力
radius:半径 スカラー
sphere_center : 中心座標のxyz numpyのarray
"""
point_list = []
"""球面の点群を作成していく"""
for i in range(360):
i = i * np.pi / 180 #ラジアン表記にする
for j in range(360):
j = j * np.pi / 180 #ラジアン表記にする
point = radius * np.array([np.sin(i) * np.cos(j),np.sin(i) * np.sin(j), np.cos(i)]) + sphere_center
#座標点を追加していく
point_list.append(point)
point_list = np.array(point_list)
# numpyのarray形式に変換
np.savetxt('sphere.asc', point_list)
# Meshlabで読める.ascファイルに保存する
return先程のPythonインタープリタで
fitting.draw_sphere(radius, sphere_center)
# radius, sphere_centerには先程の値が入っているものとします。
とすると
「sphere.asc」に球の点データが出力されます。
これはMeshlabでインポートして開けます。
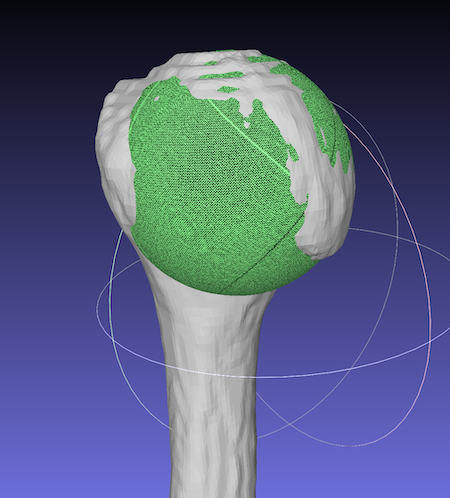
抽出した表面の部分が球に近似されたのがわかります。