こんにちは。整形外科のレオです。
私は臨床現場でプログラミングを用いているほか、
運動分析や画像解析もおこなっています。
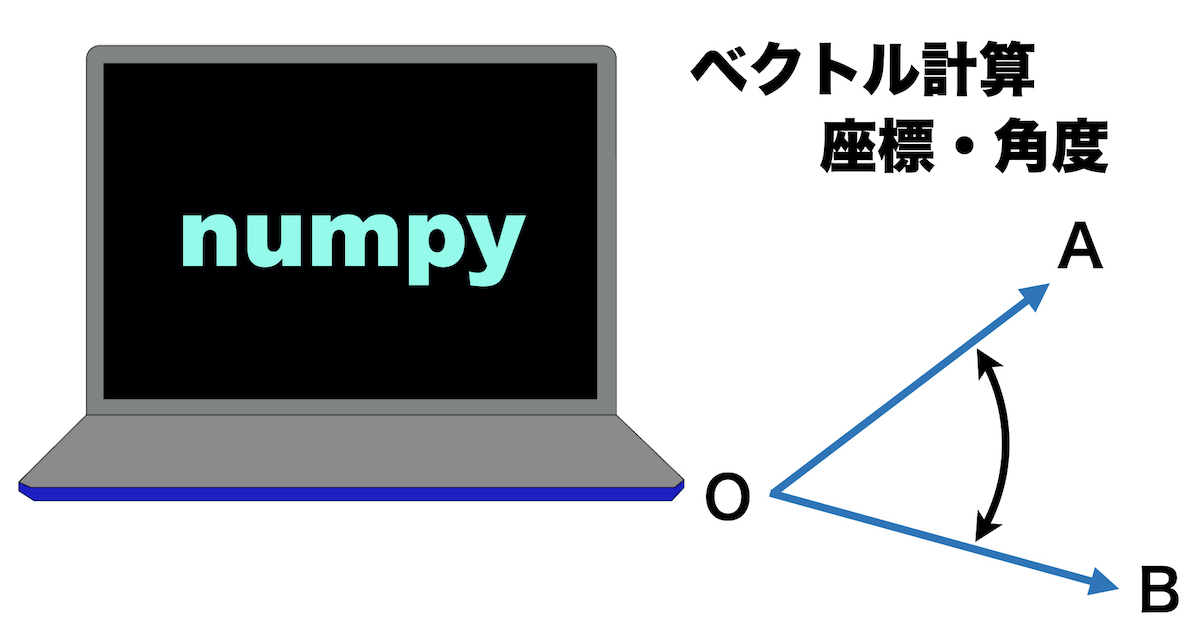
私は骨や関節の角度を計算することがあります。 そのときに便利なツールがPythonのNumpyです。
最大の利点は
「ベクトル計算が手軽にできる」
ということです。
ここでは練習として、関節のなす角度を計算します。
CTなどのデータから表面画像を作り、
MeshLabで端の点をとります。
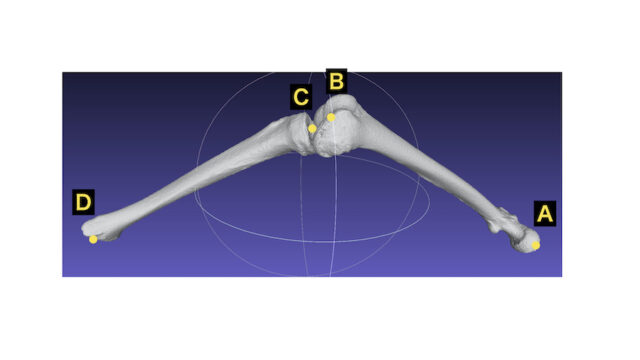
大腿骨の端を点A、B
脛骨の端を点C、D
とします。

大腿骨の軸と脛骨の軸をベクトルで表します。
ここで座標は大腿骨の向きを表すベクトルをf(femurのf), 脛骨の向きを表すベクトルをt(tibiaのt)とおきます。

大腿骨と脛骨の角度(膝が何度曲がっているか)は、これらのベクトルがなす角度になります。
大腿骨と脛骨でポイントした点はMeshLabから出力することができます。
座標は下に記載しているので、方法は知らなくても大丈夫です。
↓ 参考記事
ここでは点をとったファイルをとると下のようになっています。 x・・, y・・, z・・にあたるところが座標です。

numpyをもちいてこれらの座標から計算を行います。
原点に対する座標なので、A, B, C, Dの座標ベクトルは
\(\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}, \overrightarrow{OD}\)
で表記します。
#numpyを略称npとして使用します。
import numpy as np
#大腿骨の座標を入力
OA = np.array([ -85, 158, 1569])
OB = np.array([ -29, -67, 1187])
#脛骨の座標を入力
OC = np.array([-43, -41, 1172])
OD = np.array([-102, 125, 867]) 小数点以下は省いています。ここにある
np.array([x, y, z])
という記載で座標が定義されます。
大腿骨の方向を表すベクトル\(\vec{f} \)
脛骨の方向を表すベクトル\(\vec{t} \)
は式で書くと、
\( \vec{f} = \overrightarrow{OB} – \overrightarrow{OA} \)
\( \vec{t} = \overrightarrow{OD} – \overrightarrow{OC} \)
となります。
これをコードで書くと
f = OB - OA
t = OD - OC
print(f)
#[ 56 -225 -382]
print(t)
#[ -59 166 -305]
そのまんまですね。
ベクトルfとtのなす角は内積の公式を利用して解きます。
\( \vec{f} \cdot \vec{t} = \| \vec{f} \| \cdot \| \vec{t} \| \cdot \cos \theta \)
から
\(\cos \theta = \displaystyle \frac{\vec{f} \cdot \vec{t} }{\| \vec{f} \| \cdot \| \vec{t} \|}\)
ここで距離と内積をコードで書くと
\( \| \vec{f} \| \) は np.linalg.norm(f)
\( \vec{f} \cdot \vec{t} \)は np.dot(f, t)
と書けます。
そのため、
cos_theta = np.dot(f, t) / (np.linalg.norm(f) * np.linalg.norm(t))
print(cos_theta)
# 0.4819453868558349cosの逆関数を計算するのはnp.arccosです。
\( \theta = \arccos ( \cos \theta ) \)
theta = np.arccos(cos_theta) * 180 / np.pi
print(theta)
#61.18746444291732ここでの角度はthetaはラジアン表記(\(180° = \pi\)ラジアン)
なので、角度(°)にするために 180 / np.pi を付けています。
膝の屈曲角度は61.2°
となるわけです。
以上の計算を関数で定義する事もできます。
#ベクトルx1, x2から角度を計算する関数を定義
def angle_calc(x1, x2):
cos_theta = np.dot(x1, x2) / (np.linalg.norm(x1) * np.linalg.norm(x2))
theta = np.arccos(cos_theta) * 180 / np.pi
return theta
#関数にf, tを代入して計算する
angle_calc(f, t)
#61.18746444291732
と、f,tを入れれば角度が計算できるようになります。