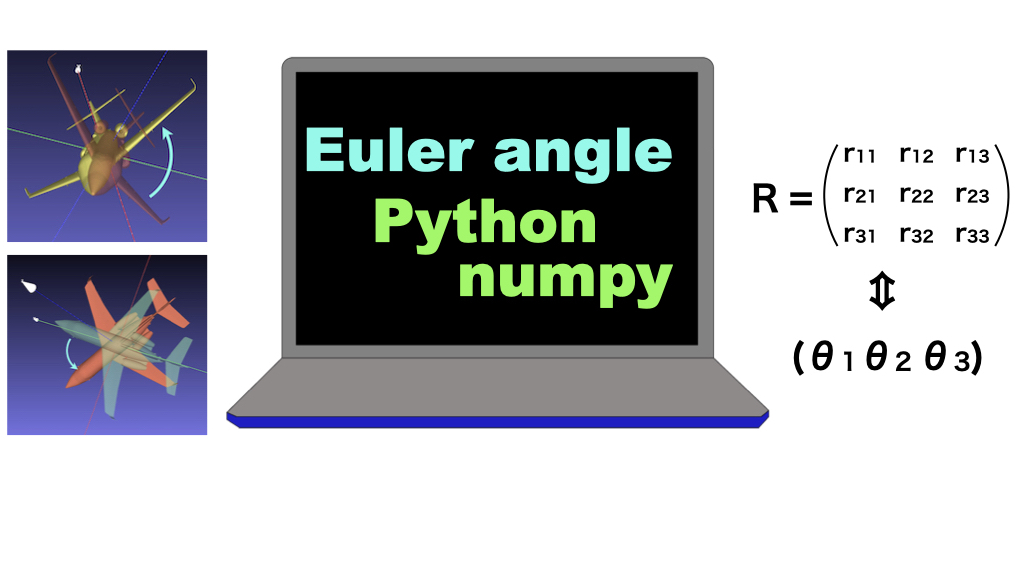
どうやって角度とか計算できるんですか?
「物体がどれくらい回転しているか(傾いているか)」
を測る方法の一つに、
「オイラー角」
という考え方があります。
私は整形外科なので、
膝の角度一つにしても
- 曲げ伸ばしの角度(屈曲伸展)
- 内股外股の角度(内反外反)
- ひねりの角度(内旋外旋)
肩の角度一つとっても
- どのくらい腕を上げたか(挙上角度)
- どちらに上げたか(挙上面角度)
- どのくらい腕をひねっているか(内旋外旋角度)
といった具合に、3つのパラメータで表す必要があります。
オイラー角はこれらのパラメータを表す、一つの表現として使われます。
=>オイラー角と回転行列の計算スクリプトはこちらでジャンプできます
3軸回りの回転
オイラー角の例として、地上にある飛行機の軸を考えます。
飛行中に回転する飛行機の向きをオイラー角で表現します。
地上での座標系を「絶対座標系」
飛行機の座標系を「ローカル座標系」
と考えます。
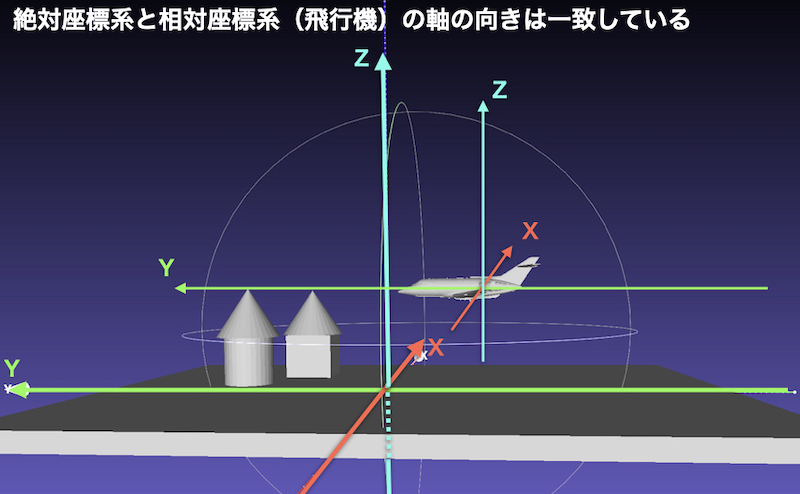
回転角度は出発時点では地上の軸(絶対座標)と一致していますが
出発後に飛行機は回転するものとします。
具体例として
「X軸回りに30度、Z軸回りに60度、Y軸回りに90度」
回転させる場合を考えます。
絶対座標系でのXYZ軸回りの回転
絶対座標系のXYZ軸回りに回転していく場合を考えます。
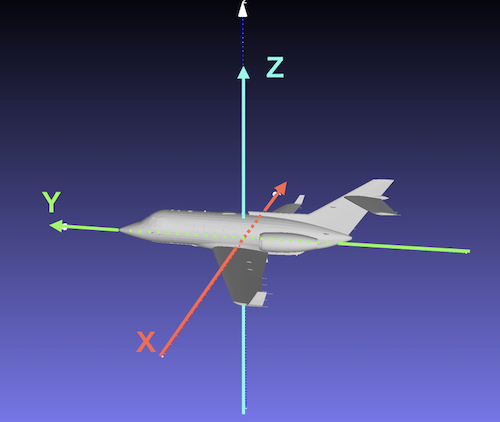
飛行機のローカル軸は左右がX軸、前後がY軸、上下がZ軸です。
飛行機が傾く時にわかっているのは、自分の座標軸だけです。
回転するときに飛行機の中の人にとっては、
「地上の座標軸のX軸まわりに30度、Z軸まわりに60度、Y軸まわりに90度回転する」
といわれても、一度回転してしまうと、飛行機からみた絶対座標の座標軸が回転してしまっているため、
大変わかりづらいです。
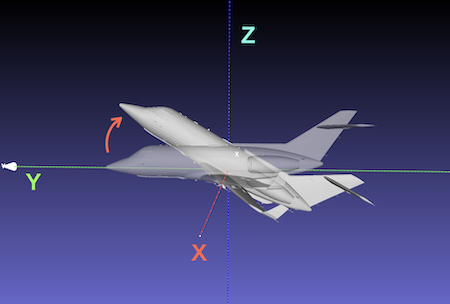
① 絶対座標のX軸回りに30度回転
始めの絶対座標のX軸は自分のローカル軸と一致しており、わかりやすい。
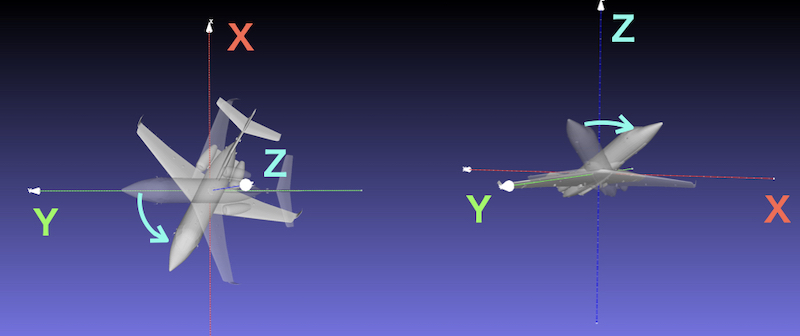
② 絶対座標のZ軸回りに60度回転
絶対座標のZ軸まわりなので傾きが認識しづらい。

③ 絶対座標のY軸回りに90度回転
ローカル軸自体が2回回転しているので、絶対座標のY軸と離れており、いよいよわかりづらい。
ローカル座標系でのXYZ軸回りの回転
かわりに
飛行機が
「自分のX軸回りに30度、Z軸回りに60度、Y軸回りに90度」
と考えたほうがわかりやすいです。
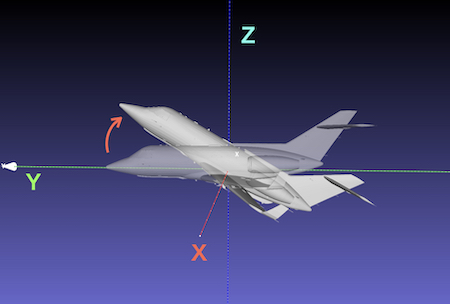
① ローカル座標のX軸まわりに30度回転
認識しやすい。絶対座標軸のときと同様
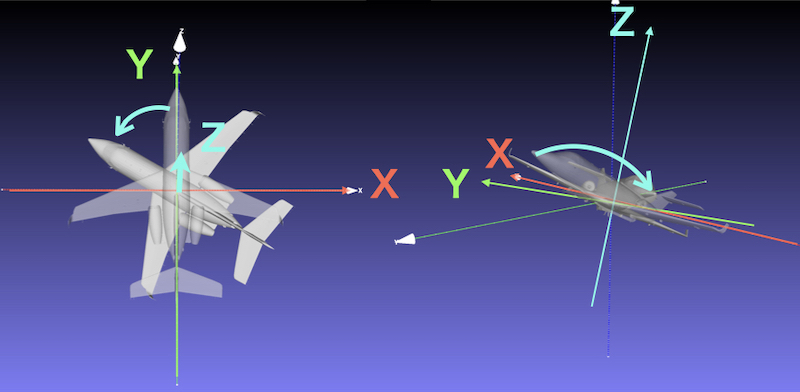
② ローカル座標のZ軸まわりに60度回転
ローカル座標軸のZ軸回り 傾いた先のZ軸まわりのため、絶対座標系の時とは異なる。
飛行機に乗っている側にはこちらのほうが認識しやすい。
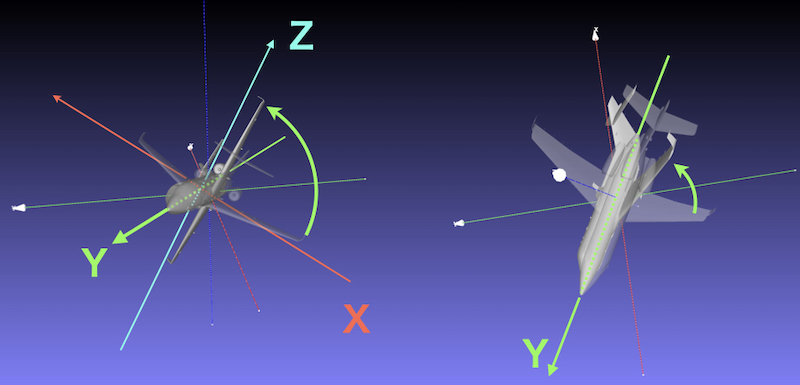
③ ローカル座標のY軸まわりに90度回転
飛行機のローカル座標系のZ軸まわりのため認識しやすい。いわゆる長軸まわりの回旋になる。
この考え方がオイラー角です。
ちなみにローカル座標系まわりに回転させた場合は、傾いた先の軸で回転するため、絶対座標系の軸まわりに回転させた時と行き着く先も変わります。
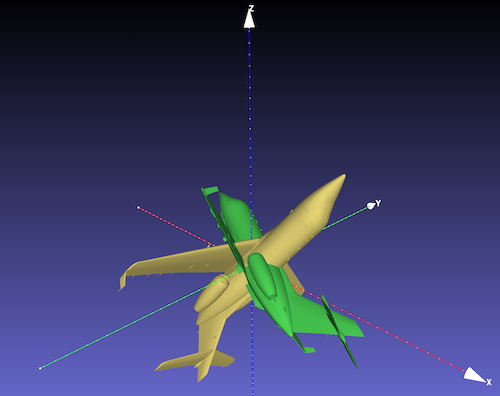
30°ー60°ー90°の順のXZY軸回転
黄色:絶対座標軸まわりの回転 緑色:ローカル座標軸まわりの回転
オイラー角の回転行列の計算方法
X, Y, Z軸回りの回転行列
詳細は専門書などにたくさん書いてありますが、ここでは直感的にわかりやすいように説明します。
まず、Z軸回り(X-Y平面上)の\(\theta\)回転を考えます。
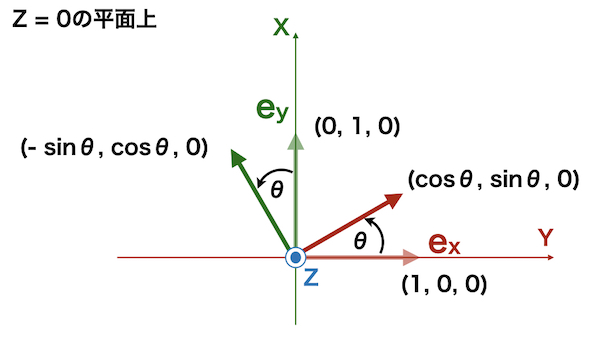
この時、
回転するベクトルは、Z軸座標には変化を与えません。
X軸の単位ベクトル\(e_x = (1, 0, 0)\)は
\((\cos \theta, \sin \theta, 0)\)
に移動します。
Y軸の単位ベクトル\(e_y = (0, 1, 0)\)は
\((-\sin \theta, \cos \theta, 0)\)
に移動します。
Z座標の単位ベクトルは\(e_z = (0, 0, 1)\)は
\((0, 0, 1)\)
のままです。
この座標変換ベクトルはこれらの単位ベクトル縦の表記で横にならべたものになるので
\(R_Z(\theta) =
(e_x, e_y, e_z) =
\begin{pmatrix}
\cos \theta & – \sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{pmatrix}\)
となります。
同様にして
\(R_X(\theta)=
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos \theta & – \sin \theta \\
0 & \sin \theta & \cos \theta
\end{pmatrix}\)
\(R_Y(\theta)=
\begin{pmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{pmatrix}\)
となります。
ローカル座標の軸回りで回転するということ
絶対座標系の軸回りX, Y, Z軸の順に回転する場合は、
\(R = R_Z \cdot R_Y \cdot R_X\)
からなる行列を対象となる点座標\((p_x, p_y, p_z)\)の左からかけて
\(\left(
\begin{array}{c}
q_x \\
q_y \\
q_z
\end{array}
\right)
=
R \cdot
\left(
\begin{array}{c}
p_x \\
p_y \\
p_z
\end{array}
\right)\)
出てきた\((q_x, q_y, q_z)\)が回転先の点になります。
しかし、この結果はローカル座標系での回転角度、回転方向とは異なります。
ローカル座標軸での回転は
「ローカル座標から見た絶対座標を回転させる行列」
を考えます。
絶対座標系とローカル座標系での相対関係は
「絶対座標でローカル軸のX軸回りにローカル座標(飛行機)を\(\theta\)回転させること」
と
「ローカル座標のX軸回りに絶対座標をー\(\theta\)回転させること」
の2つで同じです。
つまり、地上から見た飛行機の回転をオイラー角で表そうとした時、飛行機から地上が逆方向に動いているとみなしても、相対的な位置は同じです。
ですから、
ローカル座標(飛行機)を固定した座標系を考え、周囲をマイナス方向に回転させていきます
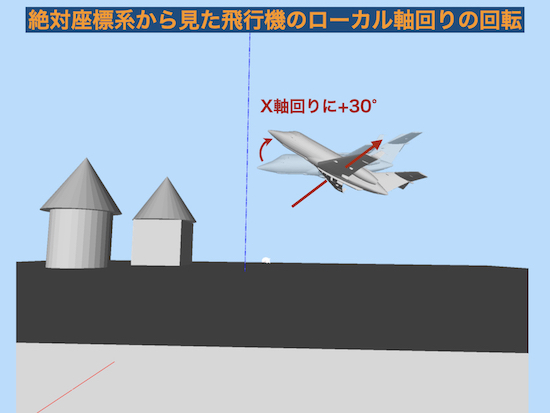
ローカル軸のX軸まわりに+30°回転は
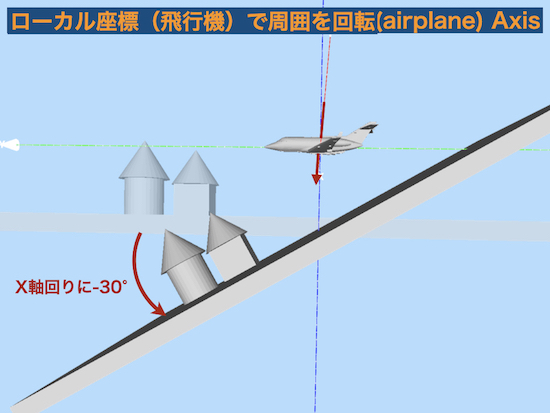
飛行機を中心として周囲をX軸回りに−30°回転
と同じ相対位置関係
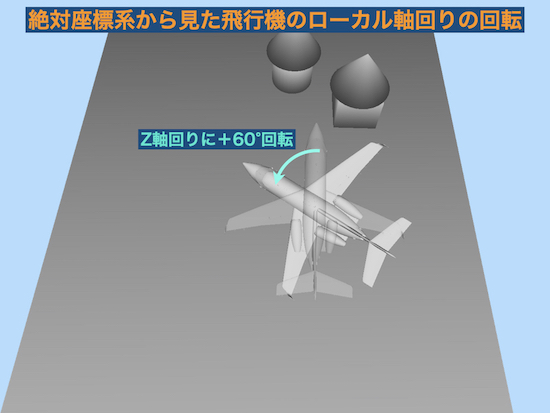
ローカル軸のZ軸まわりに+60°回転は
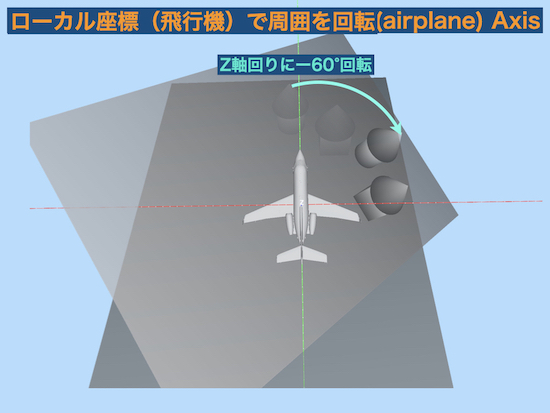
飛行機を中心として周囲をZ軸回りに−60°回転
と同じ相対位置関係
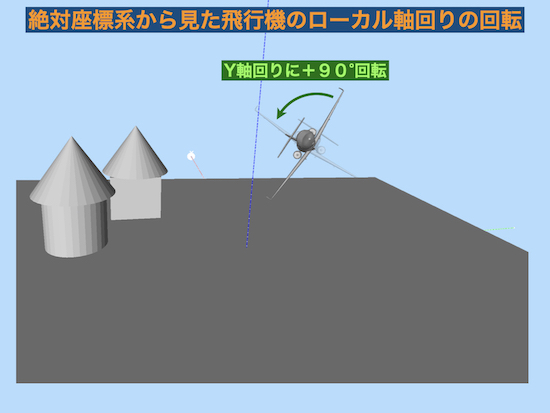
ローカル軸のY軸まわりに+90°回転は
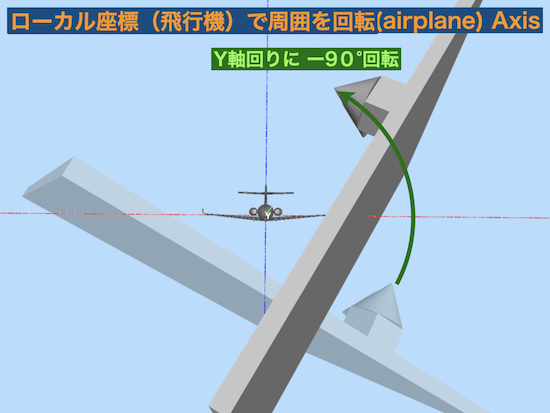
飛行機を中心として周囲をY軸回りに−90°回転
と同じ相対位置関係
そのため、ローカル座標で\(-\theta_1, -\theta_2, -\theta_3\)の順に回転させる回転行列\(R_{local}\) は、飛行機の周りに周囲の物を逆方向に回す回転行列になります。
最終的にその逆行列\(R_{global}\)を求めれば、絶対座標系で飛行機を同じ方向に回転させる行列になるわけです。
例えば、
ローカル座標系の
X, Z, Y軸まわりに順に
\(\theta_1, \theta_2, \theta_3\)回転させる行列は
ローカル座標から見て
\(R_{local} = R_Y(-\theta_3) \cdot R_Z(-\theta_2) \cdot R_X(-\theta_1)\)
となります。
この時、絶対座標からみたローカル座標の回転は、
絶対座標を回転させる回転行列の逆行列になるので
\(R_{global} = R_{local}^{-1}\)
回転行列の逆行列は転置行列で表せますので
\(R_{global} = R_{local}^{\mathrm{T}}\)
となります。
ここにXYZ軸回りの回転行列の
値を代入すると
\(R_{local} =
\begin{pmatrix}
\cos (-\theta_3) & 0 & \sin (-\theta_3) \\
0 & 1 & 0 \\
-\sin (-\theta_3) & 0 & \cos (-\theta_3)
\end{pmatrix}
\cdot
\begin{pmatrix}
\cos (-\theta_2) & – \sin (-\theta_2) & 0 \\
\sin (-\theta_2) & \cos (-\theta_2) & 0 \\
0 & 0 & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos (-\theta_1) & – \sin (-\theta_1) \\
0 & \sin (-\theta_1) & \cos (-\theta_1)
\end{pmatrix}\)
ここで
\( \cos (-\theta) = \cos \theta\)
\( \sin (-\theta) = -\sin (-\theta)\)
なので
\(R_{local} =
\begin{pmatrix}
\cos \theta_2\cos \theta_3 & \sin \theta_1\sin \theta_3 + \cos \theta_1 \cos \theta_3 \sin \theta_2 & \cos \theta_3\sin \theta_1\sin \theta_2 – \cos \theta_1\sin \theta_3\\
-\sin \theta_2 & \cos \theta_1 \cos \theta_2 & \cos \theta_2\sin \theta_1 \\
\cos \theta_2\sin \theta_3 & \cos \theta_1 \sin \theta_2 \sin \theta_3 – \cos \theta_3 \sin \theta_1 &\cos \theta_1 \cos \theta_3 + \sin \theta_1 \sin \theta_2 \sin \theta_3
\end{pmatrix}
\)
転置行列をとって
\(R_{global} =
\begin{pmatrix}
\cos \theta_2\cos \theta_3 & -\sin \theta_2 & \cos \theta_2\sin \theta_3 \\
\sin \theta_1\sin \theta_3 + \cos \theta_1 \cos \theta_3 \sin \theta_2 &\cos \theta_1 \cos \theta_2 &\cos \theta_1 \sin \theta_2 \sin \theta_3 – \cos \theta_3 \sin \theta_1 \\
\cos \theta_3\sin \theta_1\sin \theta_2 – \cos \theta_1\sin \theta_3 & \cos \theta_2\sin \theta_1& \cos \theta_1 \cos \theta_3 + \sin \theta_1 \sin \theta_2 \sin \theta_3
\end{pmatrix}
\)
これが求める回転行列
となります。
オイラー角 回転順ごとの回転行列
同じようにすべての回転順の組み合わせについて計算した回転行列は
以下のようになります。
回転行列は回転順に軸を記載する。
例えば
X軸, Z軸, Y軸の順に回転したものは\(R_{XZY}\)となる
角度は回転する順に\(\theta_1, \theta_2, \theta_3\)とし、
\(\cos\theta_1 = c_1 \cos\theta_2 = c_2 \cos\theta_3 = c_3\)
\(\sin\theta_1 = s_1 \sin\theta_2 = s_2 \sin\theta_3 = s_3\)
とおく
\(R_{XZX}=
\begin{pmatrix}
c_2 & -c_3s_2 & s_2s_3 \\
c_1s_2 & c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3 \\
s_1s_2 & c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
\(R_{XYX}=
\begin{pmatrix}
c_2 & s_2s_3 & c_3s_2 \\
s_1s_2 & c_1c_3 – c_2s_1s_3 & -c_1s_3 – c_2c_3s_1 \\
-c_1s_2 & c_3s_1 + c_1c_2s_3 & c_1c_2c_3 – s_1s_3
\end{pmatrix}\)
\(R_{YXY}=
\begin{pmatrix}
c_1c_3 – c_2s_1s_3 & s_1s_2 & c_1s_3 + c_2c_3s_1 \\
s_2s_3 & c_2 & – c_3s_2 \\
-c_3s_1 – c_1c_2s_3 & c_1s_2 & c_1c_2c_3 – s_1s_3
\end{pmatrix}\)
\(R_{YZY}=
\begin{pmatrix}
c_1c_2c_3 – s_1s_3 & -c_1s_2 & c_3s_1 + c_1c_2s_3 \\
c_3s_2 & c_2 & s_2s_3 \\
-c_1s_3 – c_2c_3s_1 & s_1s_2 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
\(R_{ZYZ}=
\begin{pmatrix}
c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3& c_1s_2 \\
c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3 & s_1s_2 \\
-c_3s_2 & s_2s_3 & c_2
\end{pmatrix}\)
\(R_{ZXZ}=
\begin{pmatrix}
c_1c_3 – c_2s_1s_3 & -c_1s_3 – c_2c_3s_1& s_1s_2 \\
c_3s_1 + c_1c_2s_3 & c_1c_2c_3 – s_1s_3 & -c_1s_2 \\
s_2s_3 & c_3s_2 & c_2
\end{pmatrix}\)
\(R_{XYZ}=
\begin{pmatrix}
c_2c_3 & -c_2s_3 & s_2 \\
c_1s_3 + c_3s_1s_2 & c_1c_3 – s_1s_2s_3 & – c_2s_1 \\
s_1s_3 – c_1c_3s_2 & c_3s_1 + c_1s_2s_3 & c_1c_2
\end{pmatrix}\)
\(R_{XZY}=
\begin{pmatrix}
c_2c_3 & -s_2 & c_2s_3 \\
s_1s_3 + c_1c_3s_2 & c_1c_2 & c_1s_2s_3 – c_3s_1 \\
c_3s_1s_2 – c_1s_3 & c_2s_1 & c_1c_3 + s_1s_2s_3
\end{pmatrix}\)
\(R_{YXZ}=
\begin{pmatrix}
c_1c_3 + s_1s_2s_3 & c_3s_1s_2 -c_1s_3 & c_2s_1 \\
c_2s_3 & c_2c_3 & – s_2 \\
c_1s_2s_3 – c_3s_1 & c_1c_3s_2 + s_1s_3 & c_1c_2
\end{pmatrix}\)
\(R_{YZX}=
\begin{pmatrix}
c_1c_2 & s_1s_3 – c_1c_3s_2 & c_3s_1 + c_1s_2s_3 \\
s_2 & c_2c_3 & – c_2s_3 \\
– c_2s_1 & c_1s_3 + c_3s_1s_2 & c_1c_3 – s_1s_2s_3
\end{pmatrix}\)
\(R_{ZYX}=
\begin{pmatrix}
c_1c_2 & c_1s_2s_3 – c_3s_1 & s_1s_3 + c_1c_3s_2 \\
c_2s_1 & c_1c_3 + s_1s_2s_3 & c_3s_1s_2 – c_1s_3 \\
– s_2 & c_2s_3 & c_2c_3
\end{pmatrix}\)
\(R_{ZXY}=
\begin{pmatrix}
c_1c_3 – s_1s_2s_3 & -c_2s_1 & c_1s_3 + c_3s_1s_2 \\
c_3s_1 + c_1s_2s_3 & c_1c_2 & s_1s_3 – c_1c_3s_2 \\
– c_2s_3 & s_2 & c_2c_3
\end{pmatrix}\)
回転行列からオイラー角の計算
回転行列の成分から回転角度
\(\theta_1, \theta_2, \theta_3\)
の計算ができます。
3×3回転行列の成分を
\(R=
\begin{pmatrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{pmatrix}\)
とします。例えば
\(R_{XZX}=
\begin{pmatrix}
c_2 & -c_3s_2 & s_2s_3 \\
c_1s_2 & c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3 \\
s_1s_2 & c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
を計算するときには
\(R_{21} = c_1s_2\)
\(R_{31} = s_1s_2\)
に注目して
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{31}}{R_{21}}\right) \)
\(R_{12} = -c_3s_2\)
\(R_{13} = s_2s_3\)
に注目して
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{12}}\right) \)
\(R_{11} = c_2\)
\(R_{21} = c_1s_2\)
求めた\(\theta_1\)を代入して
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11} \cos \theta_1}\right) \)
となり、
\(\theta_1, \theta_2, \theta_3\)
が計算されます。
ここで\(\arctan\)は-90° 〜 90°で計算されます。
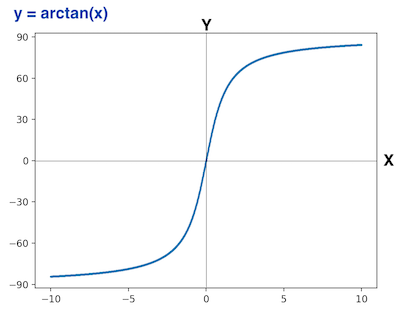
回転行列と回転角度の対応
同じようにオイラー角を回転行列の成分から求めると
\(R=
\begin{pmatrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{pmatrix}\)
とすると、
XZX回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{31}}{R_{21}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{12}}\right) \)
XYX回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{21}}{R_{31}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{11} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{12}}{R_{13}}\right) \)
YXY回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{12}}{R_{32}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{32}}{R_{22} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{21}}{R_{23}}\right) \)
YZY回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{32}}{R_{12}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{22} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{23}}{R_{21}}\right) \)
ZYZ回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{23}}{R_{13}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{13}}{R_{33} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{32}}{R_{31}}\right) \)
ZXZ回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{23}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{33} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{31}}{R_{32}}\right) \)
XZY回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{32}}{R_{22}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{12}\cos \theta_1}{R_{22} }\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{13}}{R_{11}}\right) \)
XYZ回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{33}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{13}\cos \theta_1}{R_{33}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{11}}\right) \)
YXZ回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{13}}{R_{33}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{23}\cos \theta_1}{R_{33}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{21}}{R_{22}}\right)\)
YZX回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{11}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}\cos \theta_1}{R_{11}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{22}}\right)\)
ZYX回転
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{31}\cos \theta_1}{R_{11}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{32}}{R_{33}}\right)\)
ZXY回転
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{22}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{32}\cos \theta_1}{R_{22}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{33}}\right)\)
となります。
=>次ページ 回転行列とオイラー角を求めるPythonスクリプト へ