Let’s write a python script to calculate Euler angles and rotation matrix.
=> You can also read “Euler angles intuition” Page
Calculate Rotation Matrix from Euler Angles
This script calculate the 3×3 rotation matrix from Euler angles and rotation order.
=> Table of Euler angles and Rotation matrix
import numpy as np
def rotation_matrix(theta1, theta2, theta3, order='xyz'):
"""
input
theta1, theta2, theta3 = rotation angles in rotation order (degrees)
oreder = rotation order of x,y,z e.g. XZY rotation -- 'xzy'
output
3x3 rotation matrix (numpy array)
"""
c1 = np.cos(theta1 * np.pi / 180)
s1 = np.sin(theta1 * np.pi / 180)
c2 = np.cos(theta2 * np.pi / 180)
s2 = np.sin(theta2 * np.pi / 180)
c3 = np.cos(theta3 * np.pi / 180)
s3 = np.sin(theta3 * np.pi / 180)
if order == 'xzx':
matrix=np.array([[c2, -c3*s2, s2*s3],
[c1*s2, c1*c2*c3-s1*s3, -c3*s1-c1*c2*s3],
[s1*s2, c1*s3+c2*c3*s1, c1*c3-c2*s1*s3]])
elif order=='xyx':
matrix=np.array([[c2, s2*s3, c3*s2],
[s1*s2, c1*c3-c2*s1*s3, -c1*s3-c2*c3*s1],
[-c1*s2, c3*s1+c1*c2*s3, c1*c2*c3-s1*s3]])
elif order=='yxy':
matrix=np.array([[c1*c3-c2*s1*s3, s1*s2, c1*s3+c2*c3*s1],
[s2*s3, c2, -c3*s2],
[-c3*s1-c1*c2*s3, c1*s2, c1*c2*c3-s1*s3]])
elif order=='yzy':
matrix=np.array([[c1*c2*c3-s1*s3, -c1*s2, c3*s1+c1*c2*s3],
[c3*s2, c2, s2*s3],
[-c1*s3-c2*c3*s1, s1*s2, c1*c3-c2*s1*s3]])
elif order=='zyz':
matrix=np.array([[c1*c2*c3-s1*s3, -c3*s1-c1*c2*s3, c1*s2],
[c1*s3+c2*c3*s1, c1*c3-c2*s1*s3, s1*s2],
[-c3*s2, s2*s3, c2]])
elif order=='zxz':
matrix=np.array([[c1*c3-c2*s1*s3, -c1*s3-c2*c3*s1, s1*s2],
[c3*s1+c1*c2*s3, c1*c2*c3-s1*s3, -c1*s2],
[s2*s3, c3*s2, c2]])
elif order=='xyz':
matrix=np.array([[c2*c3, -c2*s3, s2],
[c1*s3+c3*s1*s2, c1*c3-s1*s2*s3, -c2*s1],
[s1*s3-c1*c3*s2, c3*s1+c1*s2*s3, c1*c2]])
elif order=='xzy':
matrix=np.array([[c2*c3, -s2, c2*s3],
[s1*s3+c1*c3*s2, c1*c2, c1*s2*s3-c3*s1],
[c3*s1*s2-c1*s3, c2*s1, c1*c3+s1*s2*s3]])
elif order=='yxz':
matrix=np.array([[c1*c3+s1*s2*s3, c3*s1*s2-c1*s3, c2*s1],
[c2*s3, c2*c3, -s2],
[c1*s2*s3-c3*s1, c1*c3*s2+s1*s3, c1*c2]])
elif order=='yzx':
matrix=np.array([[c1*c2, s1*s3-c1*c3*s2, c3*s1+c1*s2*s3],
[s2, c2*c3, -c2*s3],
[-c2*s1, c1*s3+c3*s1*s2, c1*c3-s1*s2*s3]])
elif order=='zyx':
matrix=np.array([[c1*c2, c1*s2*s3-c3*s1, s1*s3+c1*c3*s2],
[c2*s1, c1*c3+s1*s2*s3, c3*s1*s2-c1*s3],
[-s2, c2*s3, c2*c3]])
elif order=='zxy':
matrix=np.array([[c1*c3-s1*s2*s3, -c2*s1, c1*s3+c3*s1*s2],
[c3*s1+c1*s2*s3, c1*c2, s1*s3-c1*c3*s2],
[-c2*s3, s2, c2*c3]])
return matrixCalculate Euler angles from a Rotation Matrix
This script calculate Euler angle from a 3×3 rotation matrix and rotation order.
=> Table of Rotation matrix and Euler angles
import numpy as np is already done.
def rotation_angles(matrix, order):
"""
input
matrix = 3x3 rotation matrix (numpy array)
oreder(str) = rotation order of x, y, z : e.g, rotation XZY -- 'xzy'
output
theta1, theta2, theta3 = rotation angles in rotation order
"""
r11, r12, r13 = matrix[0]
r21, r22, r23 = matrix[1]
r31, r32, r33 = matrix[2]
if order == 'xzx':
theta1 = np.arctan(r31 / r21)
theta2 = np.arctan(r21 / (r11 * np.cos(theta1)))
theta3 = np.arctan(-r13 / r12)
elif order == 'xyx':
theta1 = np.arctan(-r21 / r31)
theta2 = np.arctan(-r31 / (r11 *np.cos(theta1)))
theta3 = np.arctan(r12 / r13)
elif order == 'yxy':
theta1 = np.arctan(r12 / r32)
theta2 = np.arctan(r32 / (r22 *np.cos(theta1)))
theta3 = np.arctan(-r21 / r23)
elif order == 'yzy':
theta1 = np.arctan(-r32 / r12)
theta2 = np.arctan(-r12 / (r22 *np.cos(theta1)))
theta3 = np.arctan(r23 / r21)
elif order == 'zyz':
theta1 = np.arctan(r23 / r13)
theta2 = np.arctan(r13 / (r33 *np.cos(theta1)))
theta3 = np.arctan(-r32 / r31)
elif order == 'zxz':
theta1 = np.arctan(-r13 / r23)
theta2 = np.arctan(-r23 / (r33 *np.cos(theta1)))
theta3 = np.arctan(r31 / r32)
elif order == 'xzy':
theta1 = np.arctan(r32 / r22)
theta2 = np.arctan(-r12 * np.cos(theta1) / r22)
theta3 = np.arctan(r13 / r11)
elif order == 'xyz':
theta1 = np.arctan(-r23 / r33)
theta2 = np.arctan(r13 * np.cos(theta1) / r33)
theta3 = np.arctan(-r12 / r11)
elif order == 'yxz':
theta1 = np.arctan(r13 / r33)
theta2 = np.arctan(-r23 * np.cos(theta1) / r33)
theta3 = np.arctan(r21 / r22)
elif order == 'yzx':
theta1 = np.arctan(-r31 / r11)
theta2 = np.arctan(r21 * np.cos(theta1) / r11)
theta3 = np.arctan(-r23 / r22)
elif order == 'zyx':
theta1 = np.arctan(r21 / r11)
theta2 = np.arctan(-r31 * np.cos(theta1) / r11)
theta3 = np.arctan(r32 / r33)
elif order == 'zxy':
theta1 = np.arctan(-r12 / r22)
theta2 = np.arctan(r32 * np.cos(theta1) / r22)
theta3 = np.arctan(-r31 / r33)
theta1 = theta1 * 180 / np.pi
theta2 = theta2 * 180 / np.pi
theta3 = theta3 * 180 / np.pi
return (theta1, theta2, theta3)Examples
Calculate Rotation Matrix ⇔ Angles
input in python interpreter
import euler
rotation_mat = euler.rotation_matrix(10, 20, 30, 'yzx')
# calculate a rotation matrix of 10° 20° 30° rotation in YZX order.
print(rotation_mat)
# [[ 0.92541658 -0.20487413 0.31879578]
# [ 0.34202014 0.81379768 -0.46984631]
# [-0.16317591 0.54383814 0.82317294]]
angles = euler.rotation_angles(rotation_mat, 'yzx')
#Calculate Euler angles of YZX order from the rotation matrix
print(angles)
# (10.0, 20.0, 29.999999999999993)
#
Rotate a STL model
A airplane STL is rotated by rotation matrix calculated from Euler angles.
The rotated models are shown in Meshlab.
numpy-stl is used
numpy-stl is a library to manipulate stl and installed by ‘pip’ command.
pip install numpy-stl
import numpy as np
from stl import mesh
# use numpy-stl
#the original model is read
airplane = mesh.Mesh.from_file('airplane.stl')
#make a 4x4 matrix and 3x3 rotation matrix is substituted
rotation_x = np.identity(4)
rotation_x[:3, :3] = euler.rotation_matrix(30, 0, 0, 'xzy')
#rotate and save the model
airplane.transform(rotation_x)
airplane.save('airplane_x.stl')
#the model rotated around X axis
#in the same way, rotate the model around Z and Y axis
airplane = mesh.Mesh.from_file('airplane.stl')
# the original stl model needs to be re-read
rotation_xz = np.identity(4)
rotation_xz[:3, :3] = euler.rotation_matrix(30, 60, 0, 'xzy')
airplane.transform(rotation_xz)
airplane.save('airplane_xz.stl')
#the model rotated around X and Z axes
airplane = mesh.Mesh.from_file('airplane.stl')
rotation_xzy = np.identity(4)
rotation_xzy[:3, :3] = euler.rotation_matrix(30, 60, 90, 'xzy')
airplane.transform(rotation_xzy)
airplane.save('airplane_xzy.stl')
#The model rotated around X, Z, and Y axes
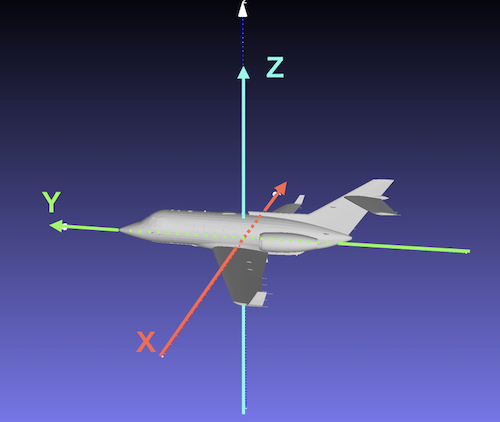
local XYZ axes of the airplane

gray: the original model(airplane.stl)
green: the model rotated around X axis(airplane_x.stl)

green: the model rotated around X axis(airplane_x.stl)
orange: the model rotated around X and Z axes(airplane_xz.stl)
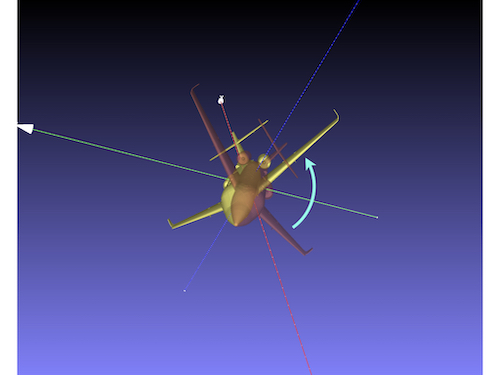
orange: the model rotated around X and Z axes(airplane_xz.stl)
yellow: the model rotated around X, Z, and Y axes(airplane_xzy.stl)
Rotation matrix calculated from three single rotation around XYZ axes
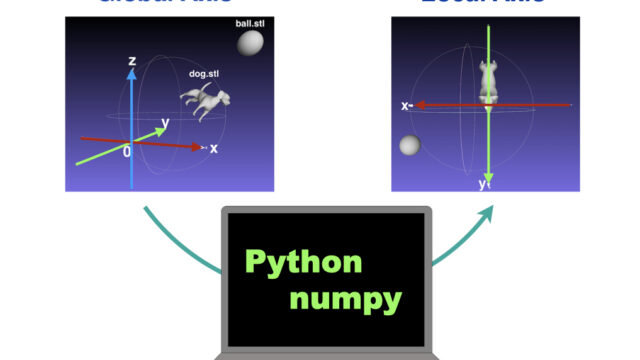
Rotation of the object around the local axes is the same as
Reverse rotation of the global world around the local object
The reverse rotation matrix can be calculated from three single rotations of \(-\theta_1, -\theta_2, -\theta_3\).
=> Intuition for “rotation around the Local Axis”
“import numpy as np” is written previously
def axis_rotation(theta, axis_name):
#calculate single rotation of \(\theta\) matrix around x,y or z
"""
input
theta = rotation angle(degrees)
axis_name = 'x', 'y' or 'z'
output
3x3 rotation matrix
"""
c = np.cos(theta * np.pi / 180)
s = np.sin(theta * np.pi / 180)
if axis_name =='x':
rotation_matrix = np.array([[1, 0, 0],
[0, c, -s],
[0, s, c]])
if axis_name =='y':
rotation_matrix = np.array([[c, 0, s],
[0, 1, 0],
[-s, 0, c]])
elif axis_name =='z':
rotation_matrix = np.array([[c, -s, 0],
[s, c, 0],
[0, 0, 1]])
return rotation_matrix
def confirm_matrix(theta1, theta2, theta3, order='xyz'):
#Calculate Rotation matrix of Euler angles from three single rotation
"""
input
theta1, theta2, theta3 = rotation angles in rotation order
order = rotation order e.g. XZY rotation -- 'xzy'
output
3x3 rotation matrix
"""
axis_name1 = order[0]
axis_name2 = order[1]
axis_name3 = order[2]
rotation1 = axis_rotation(-theta1, axis_name1)
rotation2 = axis_rotation(-theta2, axis_name2)
rotation3 = axis_rotation(-theta3, axis_name3)
# rotation matrix of global world rotation around the local object
matrix_local = np.dot(rotation3, np.dot(rotation2, rotation1))
# inverse matrix for rotation of the local object
matrix_global = matrix_local.T
return matrix_globalIn Python interpreter,
print(euler.rotation_matrix(30, 60, 90, ‘xzy’))
# [[ 3.06161700e-17 -8.66025404e-01 5.00000000e-01]
# [ 5.00000000e-01 4.33012702e-01 7.50000000e-01]
# [-8.66025404e-01 2.50000000e-01 4.33012702e-01]]
print(euler.confirm_matrix(30, 60, 90, ‘xzy’))
# [[ 3.06161700e-17 -8.66025404e-01 5.00000000e-01]
# [ 5.00000000e-01 4.33012702e-01 7.50000000e-01]
# [-8.66025404e-01 2.50000000e-01 4.33012702e-01]]
The output is the same as in the previous script
animation and numerical formula.
Let’s manipulate the STL model and write numerical formula at the same time for full understanding.