But how can I describe “3D Rotation angles of the joint”?
Calculating “Euler Angles” is one of the methods to describe rotation angles.
Euler angle is one of the ways to describe
“How much an object is rotated?”
As an orthopedic surgeon, I need to describe the joint angles in 3 directions.
For example,
the knee angles are measured in
- flexion and extension
- varus and valgus
- external and internal rotation
or
the shoulder angles are measured in
- elevation
- plane of elevation
- internal and external rotation
Euler angles can be used for joint angles.
=>Python Script to Calculate Euler Angles and Rotation Matrix
Rotation around XYZ axes
Let’s think about an airplane on the ground.
The rotation angles of the airplane will be described by using Euler angles.
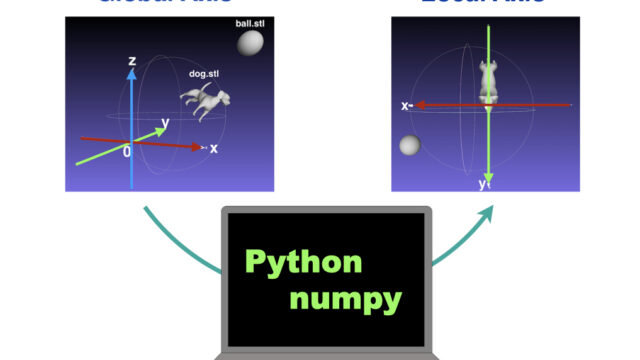
Coordinate axis on the ground is defined as
“Global axis
and
Coordinate axis of the airplane is defined as
“Local Axis
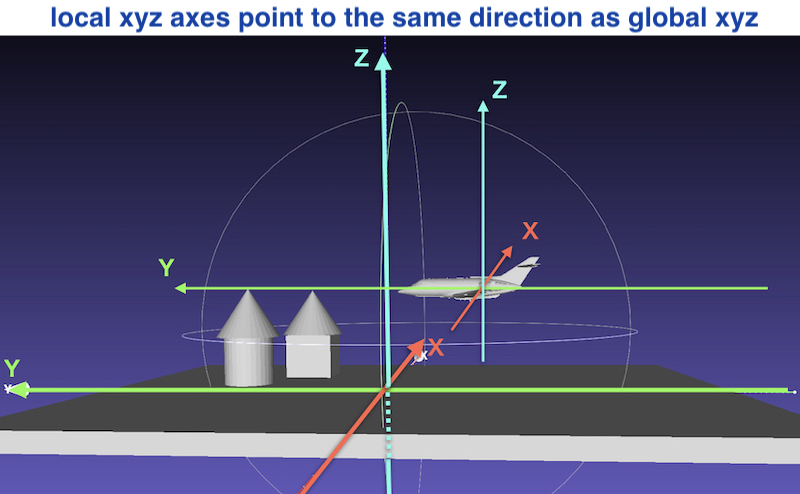
At starting position, the global axis is pointing the same directions as the local axis.
After departure, the airplane will rotate and the local axis will change.
An example of rotation
rotate 30° around X axis, 60° around Z axis and 90° around Y axis
Rotation around the Global X, Y, Z axes.
At first, let’s think about the case the airplane rotate around the global X, Y, Z axes.
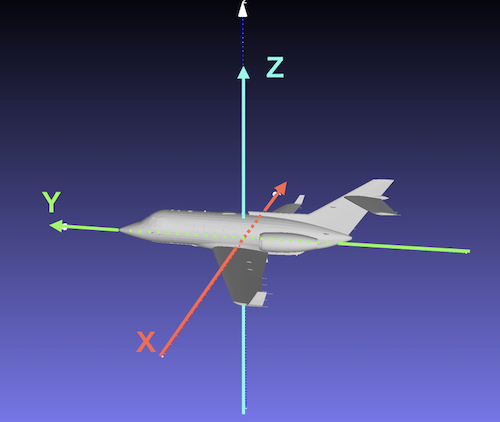
The local X axis of the airplane is pointing to right from left.
The local Y axis is pointing to the front.
The local Z axis is pointing upward.
For the pilot and passengers,
It’s difficult to understand
” rotate 30° around global X axis, rotate 60° around global Z axis, then rotate 90° around global Y axis ”
because they can only recognize the local “airplane” axes.
The latter rotations become much harder to understand.
It’s easier to understand
” rotate 30° around local X axis, rotate 60° around local axis, then rotate 90° around local Y axis ”
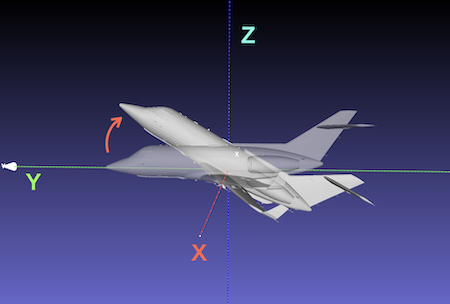
① rotate 30° around the global X axis
Easy to understand because the global and local axes are the same.
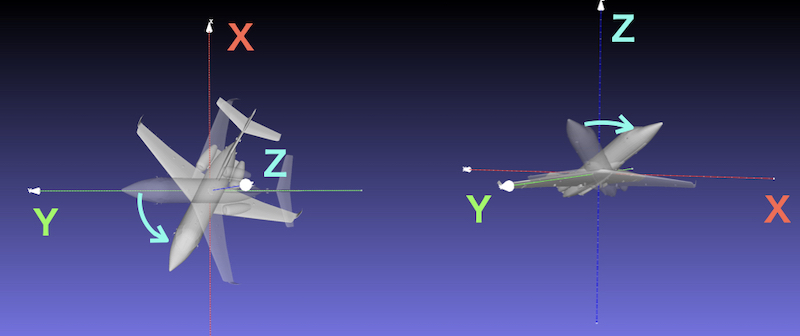
② rotate 60° around the global Z axis
Difficult to understand because the local Z axis has rotated 30°.

③ rotate 90° around the global Y axis
More difficult to recognize because the Y axis has rotated twice.
Rotation around the local XYZ axes
Now, let’s think about rotation around the Local Axis.
” Rotate 30° around the local X axis, rotate 60° around the local Z axis, and rotate 60° around the local Y axis.
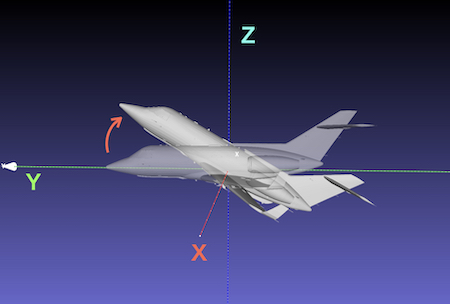
① rotate 30° around the local X axis
Easy to understand as in the global axis.
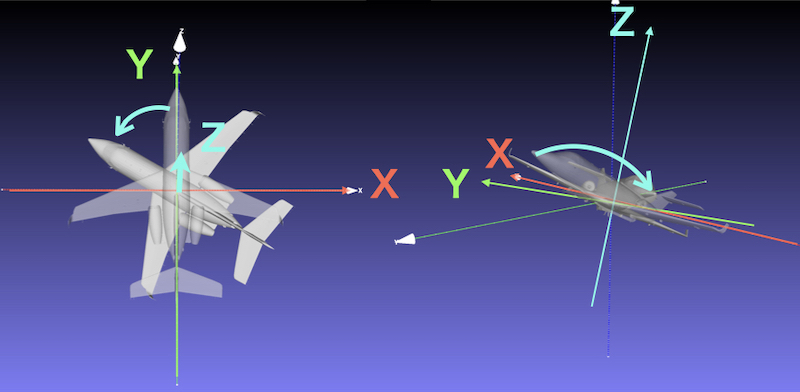
② rotate 60° around the local Z axis
Rotate around the local Z axis which has rotated in the previous rotation.
Easy to understand.
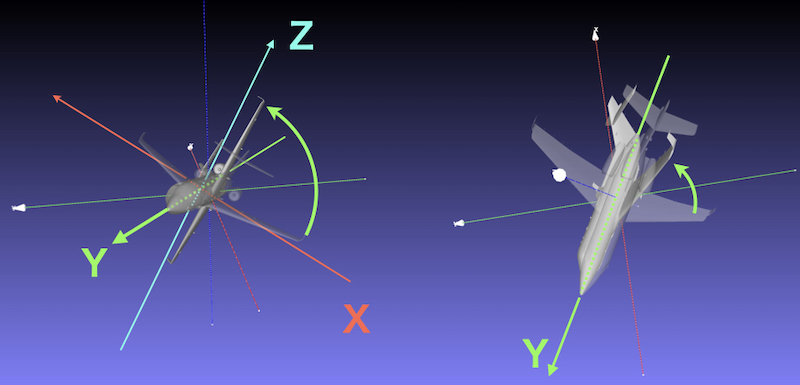
③ rotate 90° around the local Y axis
Easy to understand. Rotation around the long axis of the airplane.
The last position is different between rotation around the global axis and local axis.
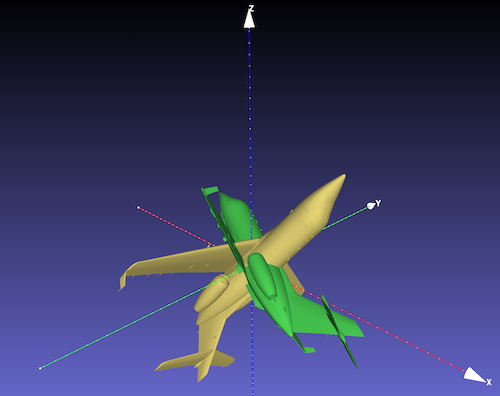
30° – 60° – 90° rotation around X-Z-Y axes
Yellow:Rotation around the Global Axis
Green : Rotation around the Local Axis
Calculate Rotation Matrix from Euler Angles
Rotation Matrix for single rotation around X, Y, Z axis
Let’s think about
“rotation \(\theta\) around the Z axis”
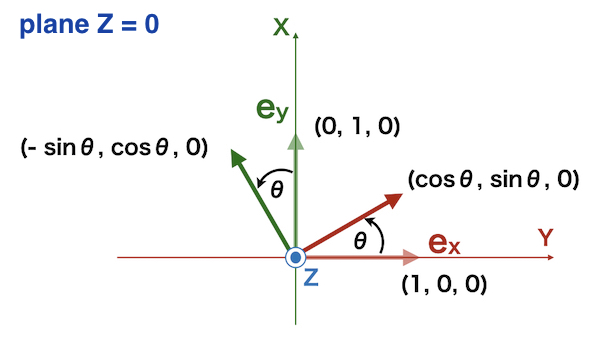
The unit vector on the X axis\(e_x = (1, 0, 0)\) moves to
\((\cos \theta, \sin \theta, 0)\)
The unit vector on the Y axis\(e_y = (0, 1, 0)\) moves to
\((-\sin \theta, \cos \theta, 0)\)
The unit vector on the Z axis \(e_z = (0, 0, 1)\) remains
\((0, 0, 1)\)
Rotation vector is bundle of the longitudinal unit vectors.
\(R_Z(\theta) =
(e_x, e_y, e_z) =
\begin{pmatrix}
\cos \theta & – \sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{pmatrix}\)
=> Rotation Matrix and Coordinate Axis
In the same way, you can calculate
\(R_X(\theta)=
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos \theta & – \sin \theta \\
0 & \sin \theta & \cos \theta
\end{pmatrix}\)
\(R_Y(\theta)=
\begin{pmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{pmatrix}\)
Intuition for “rotation around the Local Axis”
For rotation around the Global X, Y and Z,
the rotation matrix is calculated by
\(R = R_Z \cdot R_Y \cdot R_X\)
The point \(p =(p_x, p_y, p_z)\)
will be moved to
the target point \(q = (q_x, q_y, q_z)\)
by inner product of this R and p
\(\left(
\begin{array}{c}
q_x \\
q_y \\
q_z
\end{array}
\right)
=
R \cdot
\left(
\begin{array}{c}
p_x \\
p_y \\
p_z
\end{array}
\right)\)
But this result is different from the rotation around the Local Axes.
Calculate the rotation matrix which
“Rotates the Global world around the Local object”
The relative positions between the global axis and local axis does not differ between
“Rotate the local object \(\theta\) in the Global Axis”
and
“Rotate the global world – \(\theta\) around the local object (airplane)
So, we fix the local object(airplane) and rotate the global world towards minus direction.
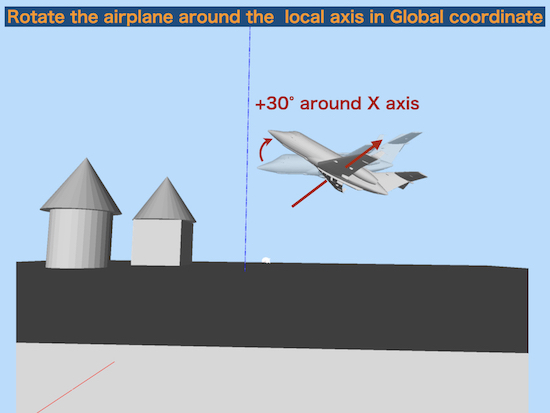
+30° rotation around the local X axis
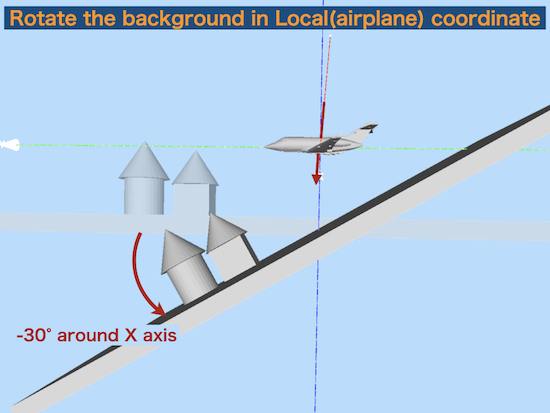
is same as
rotate the global world (background) -30° around the local object X axis(airplane).
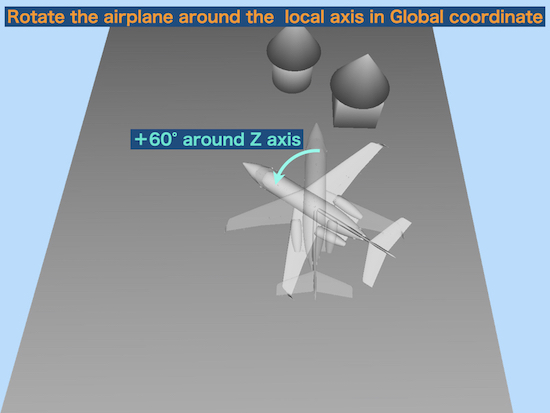
+ 60° rotation around the local Z axis
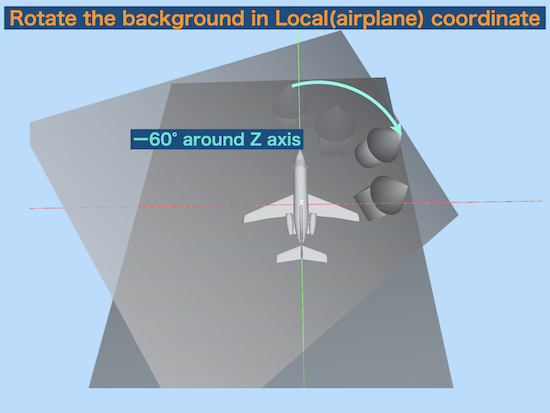
is same as
rotate the global world (background) -60° around the local object Z axis(airplane).
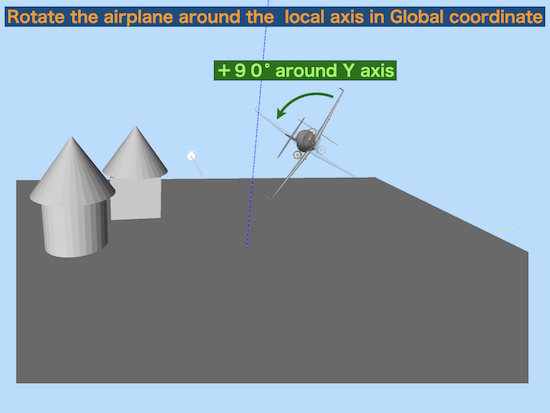
+ 90° rotation around the local Y axis
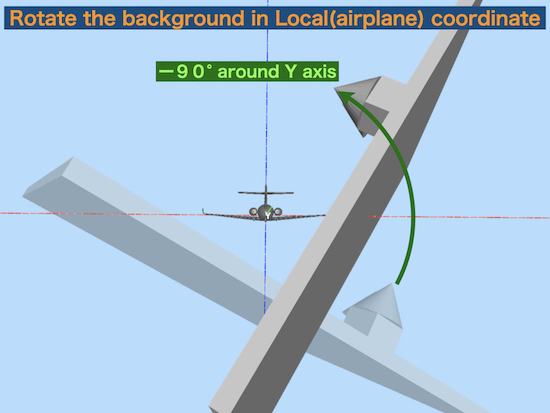
is same as
rotate the global world (background) -90° around the local object Y axis(airplane).
Overall, we should calculate \(R_{local}\) which rotates the global world \(-\theta_1, -\theta_2, -\theta_3\) around the local object.
The inverse matrix of the \(R_{local}\) is the matrix which rotates the local object around the local axes in the global coordinate system \(R_{global}\).
For example,
Let’s calculate the rotation matrix which rotates the local object around the local axis
\(\theta_1, \theta_2, \theta_3\) in X-Z-Y order.
From the local object,
\(R_{local} = R_Y(-\theta_3) \cdot R_Z(-\theta_2) \cdot R_X(-\theta_1)\)
rotates the background in the reverse direction.
From the global world, the rotation matrix which rotates the local object around the local axis is
the inverse matrix of \(R_{local}\)
\(R_{global} = R_{local}^{-1}\)
The inverse matrix of the rotation matrix is same as the transpose matrix of that.
\(R_{global} = R_{local}^{\mathrm{T}}\)
Here we calculate R_{global} from each rotation matrix,
\(R_{local} =
\begin{pmatrix}
\cos (-\theta_3) & 0 & \sin (-\theta_3) \\
0 & 1 & 0 \\
-\sin (-\theta_3) & 0 & \cos (-\theta_3)
\end{pmatrix}
\cdot
\begin{pmatrix}
\cos (-\theta_2) & – \sin (-\theta_2) & 0 \\
\sin (-\theta_2) & \cos (-\theta_2) & 0 \\
0 & 0 & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos (-\theta_1) & – \sin (-\theta_1) \\
0 & \sin (-\theta_1) & \cos (-\theta_1)
\end{pmatrix}\)
here,
\( \cos (-\theta) = \cos \theta\)
\( \sin (-\theta) = -\sin (-\theta)\)
then,
\(R_{local} =
\begin{pmatrix}
\cos \theta_2\cos \theta_3 & \sin \theta_1\sin \theta_3 + \cos \theta_1 \cos \theta_3 \sin \theta_2 & \cos \theta_3\sin \theta_1\sin \theta_2 – \cos \theta_1\sin \theta_3\\
-\sin \theta_2 & \cos \theta_1 \cos \theta_2 & \cos \theta_2\sin \theta_1 \\
\cos \theta_2\sin \theta_3 & \cos \theta_1 \sin \theta_2 \sin \theta_3 – \cos \theta_3 \sin \theta_1 &\cos \theta_1 \cos \theta_3 + \sin \theta_1 \sin \theta_2 \sin \theta_3
\end{pmatrix}
\)
transpose this matrix
\(R_{global} =
\begin{pmatrix}
\cos \theta_2\cos \theta_3 & -\sin \theta_2 & \cos \theta_2\sin \theta_3 \\
\sin \theta_1\sin \theta_3 + \cos \theta_1 \cos \theta_3 \sin \theta_2 &\cos \theta_1 \cos \theta_2 &\cos \theta_1 \sin \theta_2 \sin \theta_3 – \cos \theta_3 \sin \theta_1 \\
\cos \theta_3\sin \theta_1\sin \theta_2 – \cos \theta_1\sin \theta_3 & \cos \theta_2\sin \theta_1& \cos \theta_1 \cos \theta_3 + \sin \theta_1 \sin \theta_2 \sin \theta_3
\end{pmatrix}
\)
This is the rotation matrix for Euler angles for \(\theta_1, \theta_2, \theta_3\) in X-Z-Y order.
Table of Euler angles for each rotation
In the same way, we can calculate rotation matrices for all rotation orders.
The rotation axis is written in order.
e.g.
The rotation matrixaround the X, Z, Y axes is written as
\(R_{XZY}\)
angles are numbered as the order of rotation \(\theta_1, \theta_2, \theta_3\)
\(\cos\theta_1 = c_1 \cos\theta_2 = c_2 \cos\theta_3 = c_3\)
\(\sin\theta_1 = s_1 \sin\theta_2 = s_2 \sin\theta_3 = s_3\)
\(R_{XZX}=
\begin{pmatrix}
c_2 & -c_3s_2 & s_2s_3 \\
c_1s_2 & c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3 \\
s_1s_2 & c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
\(R_{XYX}=
\begin{pmatrix}
c_2 & s_2s_3 & c_3s_2 \\
s_1s_2 & c_1c_3 – c_2s_1s_3 & -c_1s_3 – c_2c_3s_1 \\
-c_1s_2 & c_3s_1 + c_1c_2s_3 & c_1c_2c_3 – s_1s_3
\end{pmatrix}\)
\(R_{YXY}=
\begin{pmatrix}
c_1c_3 – c_2s_1s_3 & s_1s_2 & c_1s_3 + c_2c_3s_1 \\
s_2s_3 & c_2 & – c_3s_2 \\
-c_3s_1 – c_1c_2s_3 & c_1s_2 & c_1c_2c_3 – s_1s_3
\end{pmatrix}\)
\(R_{YZY}=
\begin{pmatrix}
c_1c_2c_3 – s_1s_3 & -c_1s_2 & c_3s_1 + c_1c_2s_3 \\
c_3s_2 & c_2 & s_2s_3 \\
-c_1s_3 – c_2c_3s_1 & s_1s_2 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
\(R_{ZYZ}=
\begin{pmatrix}
c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3& c_1s_2 \\
c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3 & s_1s_2 \\
-c_3s_2 & s_2s_3 & c_2
\end{pmatrix}\)
\(R_{ZXZ}=
\begin{pmatrix}
c_1c_3 – c_2s_1s_3 & -c_1s_3 – c_2c_3s_1& s_1s_2 \\
c_3s_1 + c_1c_2s_3 & c_1c_2c_3 – s_1s_3 & -c_1s_2 \\
s_2s_3 & c_3s_2 & c_2
\end{pmatrix}\)
\(R_{XYZ}=
\begin{pmatrix}
c_2c_3 & -c_2s_3 & s_2 \\
c_1s_3 + c_3s_1s_2 & c_1c_3 – s_1s_2s_3 & – c_2s_1 \\
s_1s_3 – c_1c_3s_2 & c_3s_1 + c_1s_2s_3 & c_1c_2
\end{pmatrix}\)
\(R_{XZY}=
\begin{pmatrix}
c_2c_3 & -s_2 & c_2s_3 \\
s_1s_3 + c_1c_3s_2 & c_1c_2 & c_1s_2s_3 – c_3s_1 \\
c_3s_1s_2 – c_1s_3 & c_2s_1 & c_1c_3 + s_1s_2s_3
\end{pmatrix}\)
\(R_{YXZ}=
\begin{pmatrix}
c_1c_3 + s_1s_2s_3 & c_3s_1s_2 -c_1s_3 & c_2s_1 \\
c_2s_3 & c_2c_3 & – s_2 \\
c_1s_2s_3 – c_3s_1 & c_1c_3s_2 + s_1s_3 & c_1c_2
\end{pmatrix}\)
\(R_{YZX}=
\begin{pmatrix}
c_1c_2 & s_1s_3 – c_1c_3s_2 & c_3s_1 + c_1s_2s_3 \\
s_2 & c_2c_3 & – c_2s_3 \\
– c_2s_1 & c_1s_3 + c_3s_1s_2 & c_1c_3 – s_1s_2s_3
\end{pmatrix}\)
\(R_{ZYX}=
\begin{pmatrix}
c_1c_2 & c_1s_2s_3 – c_3s_1 & s_1s_3 + c_1c_3s_2 \\
c_2s_1 & c_1c_3 + s_1s_2s_3 & c_3s_1s_2 – c_1s_3 \\
– s_2 & c_2s_3 & c_2c_3
\end{pmatrix}\)
\(R_{ZXY}=
\begin{pmatrix}
c_1c_3 – s_1s_2s_3 & -c_2s_1 & c_1s_3 + c_3s_1s_2 \\
c_3s_1 + c_1s_2s_3 & c_1c_2 & s_1s_3 – c_1c_3s_2 \\
– c_2s_3 & s_2 & c_2c_3
\end{pmatrix}\)
Calculate Euler angles from rotation matrix
Once the rotation order is decided,
rotation angles \(\theta_1, \theta_2, \theta_3\) are calculated from a rotation matrix
The elements of a 3×3 rotation matrix is numbered as
\(R=
\begin{pmatrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{pmatrix}\)
for example,
\(R_{XZX}=
\begin{pmatrix}
c_2 & -c_3s_2 & s_2s_3 \\
c_1s_2 & c_1c_2c_3 – s_1s_3 & -c_3s_1 – c_1c_2s_3 \\
s_1s_2 & c_1s_3 + c_2c_3s_1 & c_1c_3 – c_2s_1s_3
\end{pmatrix}\)
We focus on
\(R_{21} = c_1s_2\)
\(R_{31} = s_1s_2\)
the \(\theta_1\) is calculated
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{31}}{R_{21}}\right) \)
Next, we focus
\(R_{12} = -c_3s_2\)
\(R_{13} = s_2s_3\)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{12}}\right) \)
\(R_{11} = c_2\)
\(R_{21} = c_1s_2\)
\(\theta_1\) is substituted,
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11} \cos \theta_1}\right) \)
all
\(\theta_1, \theta_2, \theta_3\)
were calculated.
Here, the result of \(\arctan\) ranged -90° 〜 90°
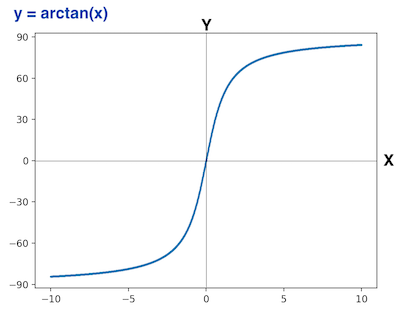
Table of Euler Angles from Rotation Matrix
In the same way, all orders of Euler angles are calculated from a rotation matrix.
\(R=
\begin{pmatrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{pmatrix}\)
XZX
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{31}}{R_{21}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{12}}\right) \)
XYX
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{21}}{R_{31}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{11} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{12}}{R_{13}}\right) \)
YXY
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{12}}{R_{32}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{32}}{R_{22} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{21}}{R_{23}}\right) \)
YZY
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{32}}{R_{12}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{22} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{23}}{R_{21}}\right) \)
ZYZ
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{23}}{R_{13}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{13}}{R_{33} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{32}}{R_{31}}\right) \)
ZXZ
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{13}}{R_{23}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{33} \cos \theta_1}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{31}}{R_{32}}\right) \)
XZY
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{32}}{R_{22}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{12}\cos \theta_1}{R_{22} }\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{13}}{R_{11}}\right) \)
XYZ
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{33}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{13}\cos \theta_1}{R_{33}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{11}}\right) \)
YXZ
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{13}}{R_{33}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{23}\cos \theta_1}{R_{33}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{21}}{R_{22}}\right)\)
YZX
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{11}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{21}\cos \theta_1}{R_{11}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{23}}{R_{22}}\right)\)
ZYX
\(\theta_1 = \arctan \displaystyle \left(\frac{R_{21}}{R_{11}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(-\frac{R_{31}\cos \theta_1}{R_{11}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(\frac{R_{32}}{R_{33}}\right)\)
ZXY
\(\theta_1 = \arctan \displaystyle \left(-\frac{R_{12}}{R_{22}}\right) \)
\(\theta_2 = \arctan \displaystyle \left(\frac{R_{32}\cos \theta_1}{R_{22}}\right) \)
\(\theta_3 = \arctan \displaystyle \left(-\frac{R_{31}}{R_{33}}\right)\)
=>Python Script to calculate Euler Angles and Rotation Matrix