ICP(Iterative Closest Point)
is an algorithm to match two point clouds.
1.Intuition of the ICP algorithm
ICP algorithm moves one point clouds to another step by step.
This algorithm is also used to match two surface data those contain point clouds.
Example of the ICP algorithm for the surface data of two dogs.
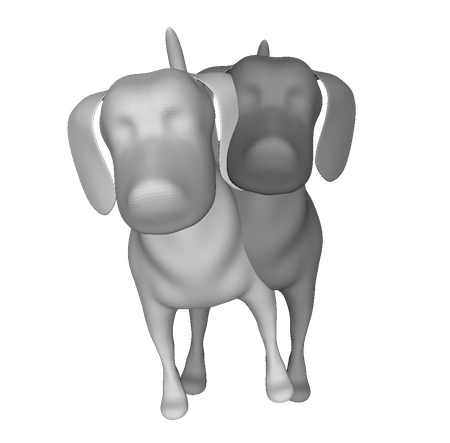
downloaded from https://free3d.com/3d-model/dog-v2–703191.html
The matching process is performed by step-by-step.
One step is called as “iteration”.
This example is done in 15 steps.

The number of the steps is set
like
- Setting a threshold for average surface distance
- Setting maximum iteration (e.g. 20)
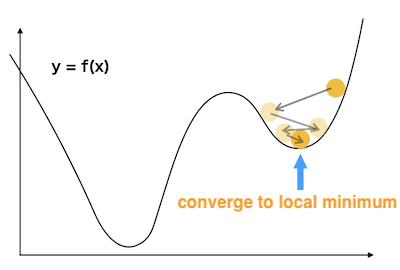
2.Problem of the “Local Minimums”
ICP can be used for only when
one surface is close to another.
This problem is common for optimization algorithms.
The process is stopped(converged) in a local minimum point.
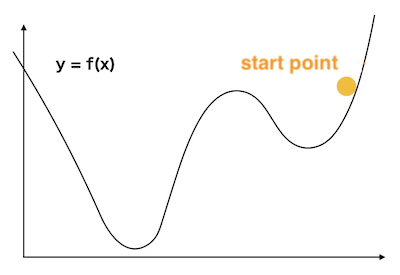
“What is local minimum point?”
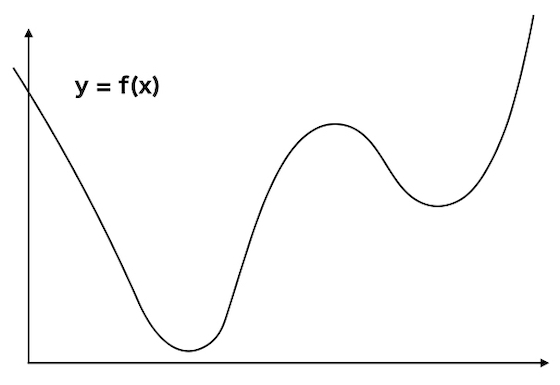
Let’s think about an example algorithm like
“Release a ball on the slope. And the end point is defined as the minimum value.”
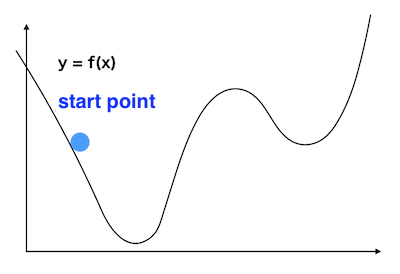
When the start point is close to the minimum value, the end point is the same as the true minimum value.
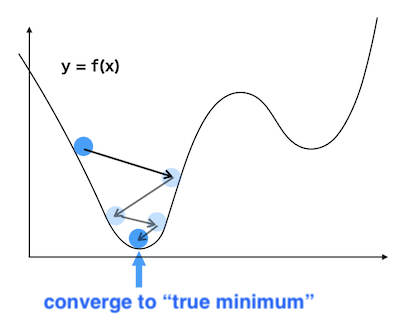
But when the start is far from the minimum value,
the ball will stop at
“Local Minimum”
which takes minimum value in a partial range.
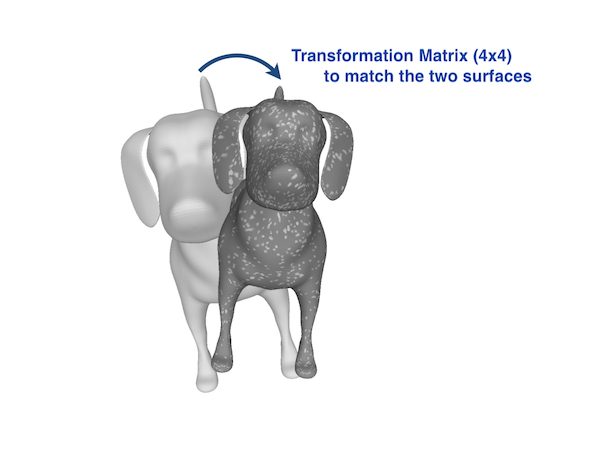
Let’s go back to the example of the two dogs.

before ICP algorithm : start from a distant point

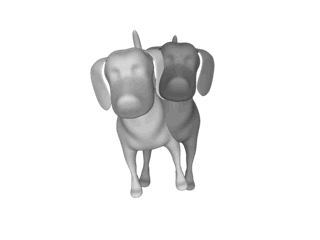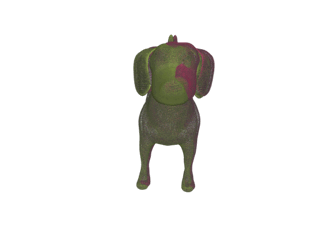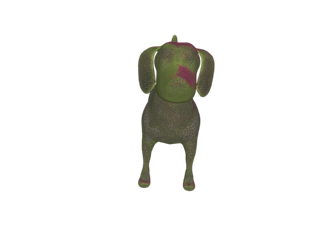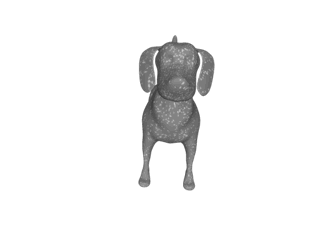
after ICP : two surfaces are overlapped, but not matched well.
To avoid this process, the two surfaces should be set close before the ICP algorithm.
=> Rough matching using three reference points
3.Script for ICP algorithm
Write a script using Python.
Goal : Get rotation matrix and translation vector used to match two surfaces in ICP algorithm
beforehand, vtk(the Visualization Toolkit) library is installed.
pip install vtk
Vtk is an useful library. But it is difficult to fully understand the structure.
This script is written for simple usage for surface matching.
ICP algorithm script using python, vtk
required : numpy, numpy-stl, vtk
reference:example of vtk-python in kitware homepage
import numpy as np
import vtk
from stl import mesh
def main(source_stl, target_stl, max_iteration=20):
"""
input
source_stl:source surface data(.stl), target_stl:target surface data (.stl)
max_iteration : the max number of steps.
output
result_matrix (4x4 matrix for transformation)
the postICP- source file will be saved as -----postICP.stl
"""
# stl data are changed into vtk.polyData for vtk (stl2vtkpoints is defined below)
source_vtk_data = stl2vtkpoints(source_stl)
target_vtk_data = stl2vtkpoints(target_stl)
# ============ run ICP ==============
icp = vtk.vtkIterativeClosestPointTransform()
#set input and output data
icp.SetSource(source_vtk_data)
icp.SetTarget(target_vtk_data)
# other setting commands
icp.GetLandmarkTransform().SetModeToRigidBody()
icp.DebugOn()
icp.SetMaximumNumberOfIterations(max_iteration)
icp.StartByMatchingCentroidsOff()
icp.Modified()
icp.Update()
#output 4x4 matrix from the icp result
icpTransformFilter = vtk.vtkTransformPolyDataFilter()
transform_matrix = icpTransformFilter.GetTransform().GetMatrix()
result_matrix = np.identity(4)
for i in range(4):
for j in range(4):
result_matrix[i][j] = transform_matrix.GetElement(i, j)
#transform the source surface using numpy-stl
source_mesh = mesh.Mesh.from_file(source_stl)
source_mesh.transform(result_matrix)
source_mesh.save(source_stl.replace('.stl','_postICP.stl'))
#saved as ---postICP.stl
return result_matrix
#return transformation matrix
def stl2vtkpoints(stl_file):
# change stl data into vtk polydata
stl_data = mesh.Mesh.from_file(stl_file)
stl_points =stl_data.points.reshape([-1, 3])
vtk_data = vtk.vtkPolyData()
vtk_data_points = vtk.vtkPoints()
vtk_data_vertices = vtk.vtkCellArray()
for point in stl_points:
id = vtk_data_points.InsertNextPoint(point)
vtk_data_vertices.InsertNextCell(1)
vtk_data_vertices.InsertCellPoint(id)
vtk_data.SetPoints(vtk_data_points)
vtk_data.SetVerts(vtk_data_vertices)
return vtk_data
Let’s apply this script for two dogs

import icp_python
from stl import mesh
matrix = icp_python.main('dog1.stl', 'dog2.stl')
print(matrix)
#[[ 0.9730126 -0.11119069 -0.20219573 -2.19660497]
# [ 0.09364225 0.99112002 -0.09440468 -1.35194807]
# [ 0.21089716 0.07292288 0.97478441 0.53585268]
# [ 0. 0. 0. 1. ]]
But I use numpy-stl because it’s intuitive and easier.